może wydawać się skomplikowane, ale w rzeczywistości opiera się na prostych zasadach. W przeciwieństwie do systemu dziesiętnego, który korzysta z cyfr od 0 do 9, system binarny wykorzystuje jedynie cyfry 0 i 1. Aby dodać liczby w tym systemie, najpierw należy zamienić liczby dziesiętne na postać binarną i odpowiednio je wyrównać. Następnie można przystąpić do dodawania, stosując zasady, które są łatwe do opanowania. W tym artykule przedstawimy krok po kroku proces dodawania w systemie binarnym, w tym zasady wyrównania oraz przykłady, które pomogą zrozumieć tę tematykę. Dzięki praktycznym wskazówkom i przykładom, każdy będzie mógł nauczyć się tej umiejętności i wykorzystywać ją w codziennym życiu.
Najważniejsze informacje:
- Dodawanie w systemie binarnym opiera się na cyfrach 0 i 1.
- Wyrównanie liczb binarnych jest kluczowe dla poprawnego dodawania.
- Podstawowe zasady dodawania binarnego obejmują przenoszenie wartości, gdy suma wynosi 10.
- Przykład dodawania dwóch liczb binarnych ilustruje proces krok po kroku.
- Praktyka jest niezbędna do opanowania dodawania w systemie binarnym.
Jak dodawać liczby w systemie binarnym - zasady i kroki
Dodawanie liczb w systemie binarnym opiera się na podstawowych zasadach, które są podobne do tych stosowanych w systemie dziesiętnym, ale z uwzględnieniem specyfiki systemu dwójkowego. W systemie binarnym używamy jedynie cyfr 0 i 1, co oznacza, że każda operacja dodawania wymaga zrozumienia, jak te cyfry współdziałają. Aby poprawnie wykonać dodawanie, należy najpierw zamienić liczby dziesiętne na postać binarną, a następnie wyrównać ich długość, dodając zera z lewej strony krótszej liczby.
Po wyrównaniu liczb, zapisujemy je jedna pod drugą, dbając o to, aby cyfry o tych samych wagach znajdowały się w tej samej kolumnie. Kluczowym elementem dodawania binarnego jest zrozumienie, że suma dwóch cyfr może prowadzić do przeniesienia wartości. Na przykład, gdy dodajemy 1 + 1, otrzymujemy 10 w systemie binarnym, co oznacza, że zapisujemy 0, a 1 przenosimy do następnej kolumny. Te zasady są fundamentem, na którym opiera się dodawanie w systemie binarnym.
Zrozumienie podstaw systemu binarnego - kluczowe informacje
System binarny to sposób reprezentacji liczb, który korzysta wyłącznie z dwóch cyfr: 0 i 1. Jest to podstawowy system liczbowy używany w komputerach i systemach cyfrowych, ponieważ odpowiada on na sposób, w jaki urządzenia elektroniczne przechowują i przetwarzają dane. W przeciwieństwie do systemu dziesiętnego, który używa dziesięciu cyfr (0-9), system binarny jest bardziej efektywny w obliczeniach logicznych i operacjach na danych.
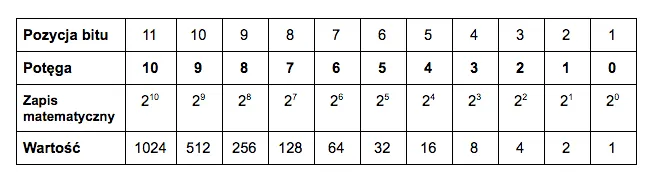
Warto zauważyć, że każda cyfra w systemie binarnym ma swoją wagę, która jest potęgą liczby 2. Na przykład, w liczbie binarnej 1011, od prawej do lewej, wagi cyfr to 1, 2, 4 i 8. Dzięki temu, system binarny może reprezentować te same wartości co system dziesiętny, ale w sposób bardziej zrozumiały dla komputerów. Zrozumienie tych podstaw jest kluczowe dla efektywnego dodawania i manipulowania liczbami w systemie binarnym.
Jak przygotować liczby do dodawania binarnego - wyrównanie i formatowanie
Aby poprawnie dodawać liczby w systemie binarnym, kluczowe jest ich odpowiednie przygotowanie. Pierwszym krokiem jest wyrównanie długości obu liczb. Jeśli jedna liczba jest krótsza, należy dodać zera z lewej strony, aby obie miały tę samą długość. Na przykład, jeśli mamy liczby 101 i 1101, to wyrównana forma pierwszej liczby będzie wyglądać jak 0101.
Następnie, po wyrównaniu, liczby zapisujemy jedna pod drugą, tak aby cyfry o tych samych wagach znajdowały się w tej samej kolumnie. To pozwala na łatwiejsze dodawanie, ponieważ możemy z łatwością porównywać odpowiadające sobie bity. Warto pamiętać, że poprawne wyrównanie i formatowanie liczb jest kluczowe dla uniknięcia błędów podczas samego procesu dodawania.
Praktyczne przykłady dodawania w systemie binarnym - krok po kroku
W tej sekcji przyjrzymy się praktycznym przykładom dodawania liczb binarnych. Zaczniemy od prostych przykładów, aby zrozumieć, jak działają zasady dodawania w systemie dwójkowym. Na przykład, dodając liczby 1010 i 1101, najpierw wyrównujemy je, a następnie dodajemy cyfra po cyfrze, stosując zasady dodawania binarnego.
Przykład dodawania 1010 i 1101 przedstawia się następująco:
| 1 0 1 0 |
| + 1 1 0 1 |
| --------- |
| 1 0 1 1 1 |
Przykład dodawania dwóch liczb binarnych - szczegółowa analiza
Rozważmy konkretny przykład dodawania dwóch liczb binarnych: 1101 i 1010. Aby wykonać operację, najpierw zapisujemy liczby jedna pod drugą, dbając o to, aby cyfry o tych samych wagach były w tej samej kolumnie. W naszym przypadku wyrównane liczby wyglądają następująco:
| 1 1 0 1 |
| + 1 0 1 0 |
| --------- |
Teraz przechodzimy do dodawania. Zaczynamy od prawej strony, dodając cyfry w każdej kolumnie. Pierwsza kolumna to 1 + 0, co daje 1. W drugiej kolumnie dodajemy 0 + 1, co również daje 1. W trzeciej kolumnie mamy 1 + 0, co znowu daje 1. W czwartej kolumnie dodajemy 1 + 1, co daje 0, a 1 przenosimy do następnej kolumny. Po uwzględnieniu przeniesienia, otrzymujemy wynik 10111, który w systemie dziesiętnym odpowiada liczbie 23.
Dodawanie większej ilości liczb binarnych - techniki i strategie
Dodawanie większej ilości liczb binarnych wymaga zastosowania kilku technik, aby efektywnie zarządzać przenoszeniem wartości. Gdy dodajemy więcej niż dwie liczby, zaczynamy od prawej strony, dodając wszystkie cyfry w danej kolumnie. Jeśli suma w danej kolumnie przekroczy 1, musimy przenieść 1 do następnej kolumny, co jest analogiczne do dodawania w systemie dziesiętnym.
Warto również stosować strategię grupowania, aby ułatwić sobie obliczenia. Możemy dodawać liczby w parach lub grupach, a następnie sumować wyniki tych grup. Dzięki temu proces dodawania staje się bardziej przejrzysty i mniej podatny na błędy. Kluczowym elementem jest także dokładne wyrównanie wszystkich liczb przed rozpoczęciem dodawania, co zapobiega pomyłkom podczas obliczeń.
Porównanie dodawania binarnego z dziesiętnym - co warto wiedzieć
Dodawanie w systemie binarnym i dziesiętnym różni się w kilku kluczowych aspektach, które warto zrozumieć, aby lepiej opanować jak dodawać w systemie binarnym. W systemie dziesiętnym używamy cyfr od 0 do 9, co daje nam dziesięć możliwych wartości w każdej kolumnie. Natomiast w systemie binarnym mamy tylko dwie cyfry: 0 i 1. To ograniczenie wpływa na sposób, w jaki wykonujemy dodawanie, ponieważ musimy stosować inne zasady przenoszenia wartości, gdy suma przekracza 1.
W dodatku, proces dodawania w systemie binarnym wymaga wyrównania długości liczb, co nie jest konieczne w systemie dziesiętnym. W przypadku dodawania binarnego, jeśli suma dwóch cyfr wynosi 10 (czyli 2 w systemie dziesiętnym), zapisujemy 0, a 1 przenosimy do następnej kolumny. Ta różnica w zasadach przenoszenia i wyrównania sprawia, że dodawanie binarne może być nieco bardziej skomplikowane, ale zrozumienie tych zasad jest kluczowe dla efektywnego wykonywania operacji w tym systemie.
Różnice między systemami - zrozumienie koncepcji dodawania
W systemie binarnym dodawanie opiera się na prostych zasadach, które różnią się od tych w systemie dziesiętnym. Kluczową różnicą jest to, że w systemie binarnym przeniesienie wartości występuje przy sumie 2, co nie ma miejsca w systemie dziesiętnym, gdzie przenosimy przy sumie 10. Ponadto, w systemie binarnym każda cyfra ma wagę, która jest potęgą liczby 2, co sprawia, że dodawanie wymaga zrozumienia, jak te wagi wpływają na wynik. Dodatkowo, proces wyrównania liczb przed dodawaniem jest istotny, aby uniknąć błędów w obliczeniach.
Jak unikać najczęstszych błędów podczas dodawania binarnego
Podczas dodawania binarnego istnieje kilka powszechnych błędów, które mogą prowadzić do niepoprawnych wyników. Jednym z najczęstszych problemów jest niewłaściwe wyrównanie liczb, co może prowadzić do błędnych obliczeń. Ważne jest, aby upewnić się, że wszystkie liczby są odpowiednio wyrównane przed rozpoczęciem dodawania. Innym częstym błędem jest nieprawidłowe przenoszenie wartości – należy pamiętać, że przeniesienie występuje, gdy suma w danej kolumnie wynosi 2. Warto również podwójnie sprawdzić swoje obliczenia, aby uniknąć pomyłek, które mogą się zdarzyć w trakcie dodawania.
Ćwiczenia praktyczne z dodawania w systemie binarnym - sprawdź swoje umiejętności
Aby lepiej zrozumieć jak dodawać w systemie binarnym, warto przećwiczyć kilka zadań. Proponowane ćwiczenia obejmują dodawanie różnych par liczb binarnych, takich jak 1010 + 1101 oraz 0110 + 0011. Staraj się wyrównywać liczby przed dodawaniem i stosować zasady przenoszenia, aby uzyskać poprawne wyniki. Regularne ćwiczenie pomoże w opanowaniu techniki dodawania w systemie binarnym.
Po wykonaniu zadań, warto sprawdzić swoje odpowiedzi, aby upewnić się, że wszystko zostało wykonane poprawnie. Można to zrobić, porównując wyniki z przykładowymi rozwiązaniami, które będą omówione w kolejnej sekcji. Dzięki temu zyskasz pewność siebie w dodawaniu binarnym i będziesz w stanie stosować tę umiejętność w praktyce.
Propozycje zadań do samodzielnego rozwiązania - rozwijaj wiedzę
Oto kilka zadań, które pomogą Ci w praktycznym zastosowaniu wiedzy na temat dodawania binarnego. Spróbuj dodać następujące liczby:
- 1101 + 1010
- 0110 + 0011
- 1001 + 0111
- 0001 + 1110
Każde z tych zadań wymaga odpowiedniego wyrównania i zastosowania zasad przenoszenia. Pamiętaj, aby dokładnie sprawdzić swoje wyniki po ich obliczeniu.
Rozwiązania zadań - krok po kroku z wyjaśnieniami
Rozpocznijmy od rozwiązania pierwszego zadania: 1101 + 1010. Wyrównujemy liczby:
| 1 1 0 1 |
| + 1 0 1 0 |
| --------- |
Dodajemy kolumny od prawej do lewej: 1 + 0 = 1, 0 + 1 = 1, 1 + 0 = 1, a w ostatniej kolumnie 1 + 1 = 0, przenosimy 1. Ostateczny wynik to 10111.
Podobnie możesz rozwiązać pozostałe zadania, stosując te same zasady. Po zakończeniu warto porównać swoje wyniki z rozwiązaniami, aby upewnić się, że wszystko zostało wykonane poprawnie.
Jak wykorzystać dodawanie binarne w programowaniu i technologii
Dodawanie binarne ma kluczowe znaczenie nie tylko w matematyce, ale także w programowaniu i technologii. Wiele języków programowania, takich jak C, C++ czy Python, wykorzystuje operacje binarne do efektywnego przetwarzania danych. Przykładem zastosowania dodawania binarnego w programowaniu jest operacja dodawania wartości w tablicach lub strukturach danych, gdzie liczby są często reprezentowane w formie binarnej. Zrozumienie zasad dodawania binarnego pozwala programistom na optymalizację algorytmów, co prowadzi do szybszego przetwarzania danych.
W przyszłości, rozwój technologii takich jak sztuczna inteligencja i uczenie maszynowe będzie wymagał coraz większej znajomości operacji binarnych. W miarę jak algorytmy stają się bardziej złożone, umiejętność efektywnego zarządzania danymi w formie binarnej stanie się niezbędna. Dlatego warto inwestować czas w naukę i praktykowanie dodawania w systemie binarnym, aby być przygotowanym na nadchodzące wyzwania w dziedzinie technologii.