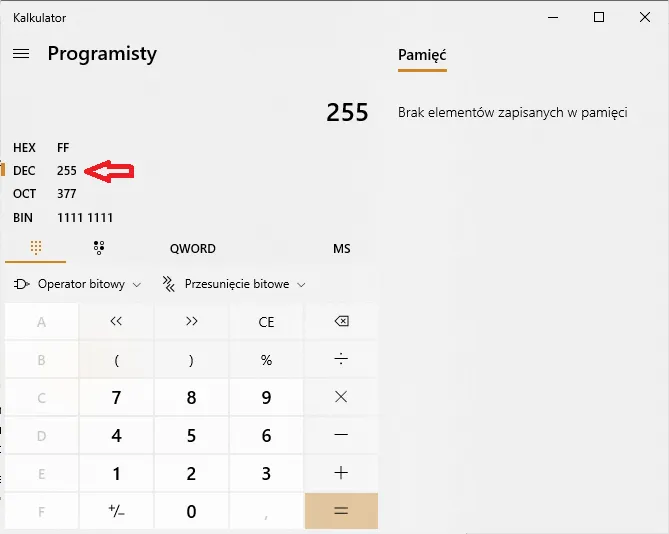
może wydawać się skomplikowane, ale w rzeczywistości jest to prosta umiejętność, którą można opanować. System binarny używa tylko dwóch cyfr: 0 i 1, a każda pozycja w liczbie reprezentuje potęgę liczby 2. Zrozumienie tego podstawowego założenia jest kluczem do przeliczania liczb binarnych na dziesiętne i odwrotnie. W tym artykule przedstawimy krok po kroku, jak łatwo i skutecznie wykonywać te konwersje oraz jak unikać typowych błędów.
Ważne jest, aby znać metody, które pozwolą na szybkie i poprawne przeliczanie liczb. Dzięki prostym technikom, takim jak dzielenie przez 2 czy sumowanie potęg, każdy może nauczyć się liczyć w systemie binarnym. W kolejnych częściach artykułu zaprezentujemy praktyczne przykłady oraz wskazówki, które pomogą w uniknięciu powszechnych pomyłek.
Kluczowe informacje:
- System binarny składa się tylko z cyfr 0 i 1, co czyni go podstawą dla komputerów.
- Aby przeliczyć liczbę binarną na dziesiętną, należy zsumować wartości potęg liczby 2 dla pozycji z cyfrą 1.
- Przykład konwersji: liczba binarna 101101 to 45 w systemie dziesiętnym.
- Przy konwersji liczby dziesiętnej na binarną, dzielimy ją przez 2 i zapisujemy reszty.
- Przykład konwersji: liczba 13 w systemie binarnym to 1101.
- Unikaj typowych błędów, takich jak pomijanie reszt z dzielenia lub błędne obliczenia potęg.
Jak zrozumieć system binarny i jego podstawowe zasady
System binarny jest podstawą współczesnej informatyki, używając jedynie dwóch cyfr: 0 i 1. Każda cyfra w liczbie binarnej odpowiada potędze liczby 2, co sprawia, że jest on idealny do reprezentacji danych w komputerach. W przeciwieństwie do systemu dziesiętnego, który opiera się na dziesięciu cyfrach, system binarny jest znacznie prostszy w kontekście elektroniki cyfrowej. Znajomość tego systemu jest kluczowa dla zrozumienia, jak działają komputery i inne urządzenia elektroniczne.
W systemie binarnym każda pozycja w liczbie ma swoje znaczenie, a zmiana jednej cyfry może prowadzić do całkowicie innej wartości. Na przykład, liczba binarna 1010 reprezentuje wartość dziesiętną 10, podczas gdy 1100 to 12. Właśnie to odzwierciedla, jak istotne jest zrozumienie zasad działania tego systemu, szczególnie dla tych, którzy chcą nauczyć się liczyć w systemie binarnym oraz zrozumieć jego zastosowanie w praktyce.
Co to jest system binarny i dlaczego jest ważny?
System binarny, składający się tylko z cyfr 0 i 1, jest fundamentalnym elementem technologii cyfrowej. Jego struktura pozwala na łatwe kodowanie i przechowywanie informacji w urządzeniach elektronicznych. W praktyce oznacza to, że wszystkie dane, od tekstów po obrazy, są przetwarzane w formie binarnej. Bez systemu binarnego nie byłoby możliwe funkcjonowanie komputerów, telefonów komórkowych i innych nowoczesnych technologii.
Warto również zauważyć, że system binarny jest używany nie tylko w komputerach, ale także w różnych dziedzinach, takich jak telekomunikacja czy inżynieria. Dzięki prostocie i jednoznaczności, system ten umożliwia efektywne przesyłanie i przetwarzanie danych. Zrozumienie jego podstawowych zasad jest kluczowe dla każdego, kto chce zgłębiać tajniki technologii cyfrowej.
Jak w prosty sposób przeliczać liczby binarne na dziesiętne
Aby przeliczyć liczby binarne na dziesiętne, należy zrozumieć prostą metodę, która opiera się na potęgach liczby 2. Każda cyfra w liczbie binarnej ma swoje miejsce i wartość, co pozwala na łatwe obliczenie jej odpowiednika w systemie dziesiętnym. W tej sekcji przedstawimy krok po kroku, jak skutecznie wykonać tę konwersję.
Proces konwersji polega na zsumowaniu wartości potęg liczby 2 dla każdej pozycji w liczbie binarnej, gdzie znajduje się cyfra 1. Na przykład, w liczbie binarnej 101101 każda cyfra ma przypisaną odpowiednią potęgę liczby 2. To podejście pozwala na szybkie i efektywne przeliczenie liczby, co jest niezwykle przydatne w codziennej pracy z danymi cyfrowymi.
| Liczba binarna | Liczba dziesiętna |
|---|---|
| 0001 | 1 |
| 0010 | 2 |
| 0101 | 5 |
| 0110 | 6 |
| 1010 | 10 |
| 1100 | 12 |
| 1011 | 11 |
Krok po kroku: Metoda konwersji z binarnego na dziesiętny
Metoda konwersji z binarnego na dziesiętny jest prosta i można ją zrealizować w kilku krokach. Po pierwsze, należy zapisać liczbę binarną i przypisać każdej cyfrze odpowiednią potęgę liczby 2, zaczynając od prawej strony. Na przykład, dla liczby 101101, przypisujemy potęgi: 2⁵, 2⁴, 2³, 2², 2¹, 2⁰.
Następnie, dla każdej pozycji, w której znajduje się cyfra 1, obliczamy wartość potęgi liczby 2. W przypadku liczby 101101, obliczenia będą wyglądać następująco: 1 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰. Ostatecznie, sumujemy wszystkie wartości, aby uzyskać wynik dziesiętny.
Warto pamiętać, że ta metoda jest nie tylko prosta, ale także niezwykle efektywna, co czyni ją idealną do codziennego użytku w obliczeniach związanych z systemem binarnym. Dzięki zrozumieniu tej konwersji, można łatwo przeliczać liczby i lepiej zrozumieć, jak funkcjonują urządzenia cyfrowe.
Czytaj więcej: Co to system zero-jedynkowy a binarny - zrozum różnice i zastosowania
Jak konwertować liczby dziesiętne na binarne w łatwy sposób
Aby przeliczyć liczby dziesiętne na binarne, można zastosować prostą metodę dzielenia przez 2. Ta technika polega na dzieleniu liczby dziesiętnej przez 2, a następnie zapisywaniu reszty z każdego dzielenia. Odczytując reszty od końca, uzyskujemy odpowiednik binarny. Dzięki tej metodzie, każdy może łatwo i szybko przeliczać liczby dziesiętne na system binarny.
Ważne jest, aby pamiętać, że proces ten wymaga kilku kroków. Na początku dzielimy liczbę dziesiętną przez 2, zapisując resztę. Następnie, wynik dzielenia powtarzamy, aż do momentu, gdy osiągniemy 0. Ostatecznie, odczytujemy wszystkie zebrane reszty od dołu do góry, co daje nam naszą liczbę w systemie binarnym. Ta metoda jest nie tylko prosta, ale także skuteczna, co czyni ją idealną dla wszystkich, którzy chcą łatwo liczyć w systemie binarnym.
Prosta metoda dzielenia dla przekształcenia dziesiętnego na binarny
Metoda dzielenia polega na systematycznym dzieleniu liczby dziesiętnej przez 2 i zapisywaniu reszt. Rozpoczynamy od liczby, którą chcemy przeliczyć. Na przykład, jeśli mamy liczbę 13, dzielimy ją przez 2: 13 ÷ 2 = 6, reszta to 1. Następnie dzielimy 6 przez 2, co daje 3 i resztę 0. Powtarzamy ten proces, aż dotrzemy do zera.
W przypadku liczby 13, kolejne dzielenia będą wyglądać następująco: 3 ÷ 2 = 1 (reszta 1) oraz 1 ÷ 2 = 0 (reszta 1). Zbierając reszty, otrzymujemy 1, 1, 0, 1. Odczytując je od końca, uzyskujemy wynik 1101, co oznacza, że liczba 13 w systemie binarnym to 1101. Ta metoda jest przejrzysta i łatwa do zastosowania, co czyni ją idealnym rozwiązaniem dla każdego, kto chce zrozumieć system binarny krok po kroku.
Najczęstsze błędy przy obliczeniach w systemie binarnym
Podczas wykonywania obliczeń w systemie binarnym, mogą występować różne błędy, które wpływają na ostateczne wyniki. Jednym z najczęstszych błędów jest pomylenie miejsc wartości, co prowadzi do błędnych obliczeń. Na przykład, zamiana miejscami cyfr 1 i 0 może całkowicie zmienić wartość liczby. Innym problemem jest nieprawidłowe dodawanie lub odejmowanie w systemie binarnym, które różni się od tego w systemie dziesiętnym. Warto również zauważyć, że zapominanie o resztach podczas konwersji lub obliczeń może prowadzić do błędnych wyników.
Te błędy mogą nie tylko wpłynąć na końcowy wynik, ale także wprowadzić zamieszanie w dalszych obliczeniach. Dlatego tak ważne jest, aby być świadomym tych pułapek i regularnie sprawdzać swoje obliczenia. Uważność na szczegóły oraz zrozumienie zasad działania systemu binarnego są kluczowe dla uniknięcia tych typowych problemów.
Jak unikać pomyłek przy liczeniu w systemie binarnym
Aby zminimalizować błędy przy obliczeniach w systemie binarnym, warto zastosować kilka praktycznych strategii. Po pierwsze, zawsze sprawdzaj swoje obliczenia krok po kroku, zwracając szczególną uwagę na wartości miejsc. Po drugie, warto używać papieru lub narzędzi cyfrowych do zapisywania obliczeń, co pomoże uniknąć pomyłek związanych z pamięcią. Dodatkowo, regularne ćwiczenie z różnymi przykładami pozwoli na lepsze zrozumienie zasad działania systemu binarnego.
Innym skutecznym sposobem jest uczenie się na błędach. Jeśli zauważysz, że popełniłeś jakiś błąd, spróbuj zrozumieć, co poszło nie tak, i jak możesz to poprawić w przyszłości. Wreszcie, korzystanie z pomocnych materiałów edukacyjnych lub aplikacji do nauki może znacząco poprawić Twoje umiejętności w zakresie obliczeń binarnych.
Przykłady praktyczne: Obliczenia w systemie binarnym
Praktyczne przykłady są kluczowe dla zrozumienia, jak działa system binarny. Na przykład, przeliczając liczbę binarną 1101 na system dziesiętny, możemy obliczyć: 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰, co daje 8 + 4 + 0 + 1 = 13. Innym przykładem jest liczba binarna 1010, która w systemie dziesiętnym odpowiada 10, obliczając: 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰, co daje 8 + 0 + 2 + 0 = 10.
Teraz, konwertując liczbę dziesiętną 25 na system binarny, dzielimy ją przez 2: 25 ÷ 2 = 12, reszta 1; 12 ÷ 2 = 6, reszta 0; 6 ÷ 2 = 3, reszta 0; 3 ÷ 2 = 1, reszta 1; 1 ÷ 2 = 0, reszta 1. Odczytując reszty od końca, otrzymujemy 11001. Kolejnym przykładem może być liczba 45, której binarny odpowiednik to 101101, co obliczamy jako 1 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 32 + 0 + 8 + 4 + 0 + 1 = 45.
Rozwiązywanie zadań z użyciem systemu binarnego dla lepszego zrozumienia
Aby lepiej zrozumieć system binarny, warto rozwiązywać różnorodne zadania i ćwiczenia. Przykładowo, można spróbować przeliczyć różne liczby dziesiętne na binarne, takie jak 30, 15 czy 7, a następnie zweryfikować wyniki. Można również tworzyć własne liczby binarne i próbować przeliczać je na system dziesiętny, co pozwala na lepsze zrozumienie mechanizmów działania obu systemów.
Innym ciekawym ćwiczeniem jest porównywanie wyników konwersji z użyciem różnych metod, takich jak dzielenie przez 2 oraz sumowanie potęg liczby 2. Regularne ćwiczenie z różnymi zadaniami pomoże w utrwaleniu wiedzy i umiejętności związanych z obliczeniami w systemie binarnym. Praktyka czyni mistrza, dlatego warto poświęcić czas na te zadania, aby stać się pewnym siebie w obliczeniach.
Jak wykorzystać system binarny w programowaniu i technologii
System binarny nie tylko stanowi fundament obliczeń w komputerach, ale także ma kluczowe zastosowanie w programowaniu oraz technologii informacyjnej. Rozumienie konwersji między systemami liczbowymi może być niezwykle przydatne przy pisaniu algorytmów, które operują na danych w formacie binarnym. Na przykład, programiści często muszą przekształcać liczby dziesiętne na binarne, aby efektywnie zarządzać pamięcią i wykonywać operacje bitowe, co jest istotne w kontekście optymalizacji kodu oraz zwiększania wydajności aplikacji.
Dodatkowo, znajomość systemu binarnego jest niezbędna w dziedzinach takich jak cyberbezpieczeństwo i inżynieria oprogramowania. W tych obszarach, umiejętność analizy danych binarnych może pomóc w identyfikacji luk w zabezpieczeniach oraz w tworzeniu bardziej odpornych systemów. W miarę jak technologia rozwija się, a złożoność systemów rośnie, umiejętność pracy z systemem binarnym stanie się coraz bardziej cenna, otwierając drzwi do nowych możliwości zawodowych i innowacyjnych rozwiązań. Dlatego warto inwestować czas w rozwijanie tej wiedzy i umiejętności.