Aby zamienić liczbę dziesiętną na system binarny, istnieje kilka prostych metod, które można zastosować. Najpopularniejszą z nich jest dzielenie liczby przez 2 i zapisywanie reszt z tego procesu. Powtarzając te działania, aż liczba stanie się równa 0, można uzyskać binarną reprezentację liczby. Na przykład, liczba 20 po kolejnych dzieleniach przez 2 daje nam wynik w postaci 10100 w systemie binarnym.
Inne metody konwersji obejmują operacje bitowe oraz konwersję liczb szesnastkowych na binarne. Każda z tych metod ma swoje zastosowanie, szczególnie w programowaniu, gdzie znajomość systemów liczbowych jest kluczowa. W tym artykule przedstawimy różne sposoby na zamianę liczb i podzielimy się praktycznymi przykładami kodu w popularnych językach programowania.
Najważniejsze informacje:
- Podstawową metodą konwersji jest dzielenie przez 2 i zapisywanie reszt.
- Reszty zapisywane w odwrotnej kolejności tworzą binarną reprezentację liczby.
- Inną metodą jest wykorzystanie operacji bitowych, które pozwalają na efektywną konwersję.
- Można także konwertować liczby szesnastkowe na binarne przy użyciu tabel przyporządkowujących.
- Wszystkie te metody można zaimplementować w językach programowania, takich jak C++, Java i Python.
Jak zamienić liczbę dziesiętną na system binarny prostą metodą?
Jednym z najprostszych sposobów, aby zamienić liczbę dziesiętną na system binarny, jest wykorzystanie metody dzielenia przez 2. Proces ten polega na sukcesywnym dzieleniu liczby przez 2 i zapisywaniu reszt, które powstają w trakcie dzielenia. Powtarzamy ten proces, aż liczba osiągnie wartość 0. Na koniec, reszty zapisywane w odwrotnej kolejności utworzą binarną reprezentację liczby. Przykładowo, aby zamienić liczbę 20 na system binarny, wykonujemy następujące dzielenia:
- 20 ÷ 2 = 10, reszta 0
- 10 ÷ 2 = 5, reszta 0
- 5 ÷ 2 = 2, reszta 1
- 2 ÷ 2 = 1, reszta 0
- 1 ÷ 2 = 0, reszta 1
Po zapisaniu reszt od dołu do góry, otrzymujemy wynik 10100 w systemie binarnym. Ta metoda jest nie tylko prosta, ale również bardzo efektywna, co czyni ją popularnym wyborem wśród osób uczących się konwersji liczb.
Krok po kroku: Proces dzielenia liczby przez 2 dla konwersji
Aby dokładniej zrozumieć, jak przebiega proces konwersji, warto przeanalizować go krok po kroku. Pierwszym krokiem jest podzielenie liczby przez 2. Po każdym dzieleniu zapisujemy resztę, która będzie częścią naszej binarnej reprezentacji. Ważne jest, aby pamiętać, że reszty są kluczowe, ponieważ to one definiują, jakie bity pojawią się w końcowym wyniku.
Kiedy wykonujemy dzielenia, należy mieć na uwadze, że proces ten powtarzamy, aż osiągniemy 0. Na każdym etapie zapisujemy reszty, które musimy następnie uporządkować. To właśnie odwrotna kolejność zapisanych reszt jest kluczowa przy tworzeniu binarnej reprezentacji. W przypadku liczby 20, reszty 0, 0, 1, 0, 1 tworzą ostateczny wynik 10100.
Na koniec, warto zwrócić uwagę, że metoda dzielenia przez 2 jest bardzo intuicyjna i łatwa do zrozumienia, co czyni ją idealną dla początkujących. Umożliwia ona nie tylko naukę konwersji liczb, ale także rozwija umiejętności matematyczne. Dzięki tej metodzie, każdy może nauczyć się, jak przekonwertować liczbę na format binarny w prosty sposób.
Zrozumienie reszt: Jak odczytać wyniki dzielenia dla binarnej reprezentacji
Aby skutecznie zamienić liczbę dziesiętną na system binarny, ważne jest, aby zrozumieć, jak odczytywać reszty uzyskane podczas procesu dzielenia. Kiedy dzielimy liczbę przez 2, reszta, którą otrzymujemy, wskazuje wartość najmłodszego bitu w binarnej reprezentacji. Na przykład, jeśli dzielimy liczbę 20, reszty 0, 0, 1, 0, 1 będą miały kluczowe znaczenie dla utworzenia ostatecznego wyniku. Ważne jest, aby pamiętać, że reszty muszą być zapisywane w odwrotnej kolejności, co oznacza, że ostatnia reszta stanie się pierwszym bitem w binarnym zapisie.
Podczas konwersji, reszty są kluczowym elementem, który pozwala na zbudowanie pełnej reprezentacji binarnej. Kiedy mamy już wszystkie reszty, należy je uporządkować od ostatniej do pierwszej, aby uzyskać poprawny wynik. W przypadku liczby 20, zapiszemy reszty jako 10100, co odpowiada wartości binarnej. Zrozumienie tego procesu ułatwia nie tylko konwersję liczb, ale także rozwija umiejętności matematyczne, które są niezbędne w programowaniu i informatyce.
Użycie operacji bitowych do konwersji liczby na binarną
Operacje bitowe to efektywny sposób na zamianę liczby dziesiętnej na system binarny. W tej metodzie wykorzystujemy operację AND oraz przesunięcia bitowe, aby iteracyjnie sprawdzić każdy bit liczby. Proces ten polega na sprawdzeniu najmłodszego bitu za pomocą operacji AND z wartością 1. Jeśli wynik jest równy 1, oznacza to, że dany bit jest ustawiony, a następnie przesuwamy liczbę w prawo o jeden bit, aby przejść do następnego.
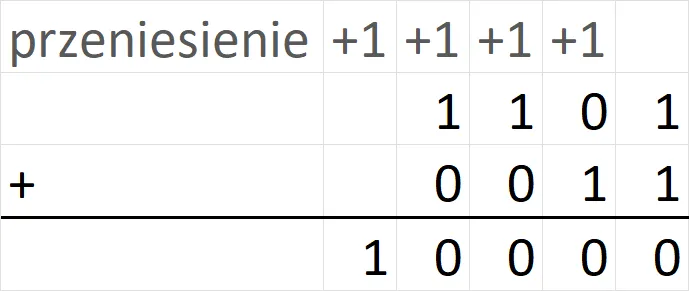
Na przykład, dla liczby 13 (w systemie dziesiętnym), w postaci binarnej to 1101. Sprawdzając najmłodszy bit, wykonujemy operację AND: 13 AND 1 = 1, co oznacza, że najmłodszy bit jest ustawiony. Następnie przesuwamy liczbę 13 w prawo, co daje nam 6 (0110 w systemie binarnym). Kontynuując ten proces, możemy uzyskać pełną reprezentację binarną liczby, zapisując wyniki w odpowiedniej kolejności.
Przekonwertowanie liczby szesnastkowej na binarną: Łatwy sposób
Konwersja liczby szesnastkowej na binarną jest równie prosta jak jej dzielenie przez 2. Każda cyfra w systemie szesnastkowym może być bezpośrednio zamieniona na czterobitowy ciąg binarny. Na przykład, cyfra A w systemie szesnastkowym odpowiada 1010 w systemie binarnym, a cyfra F to 1111. Dzięki tej metodzie, możemy szybko i efektywnie przekształcić dowolną liczbę szesnastkową na format binarny.
Poniższa tabela przedstawia konwersję cyfr szesnastkowych na ich binarne odpowiedniki:
| Cyfra szesnastkowa | Reprezentacja binarna |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Przykłady kodu: Jak zaimplementować konwersję w Pythonie
W Pythonie konwersja liczby dziesiętnej na system binarny jest bardzo prosta i intuicyjna. Możemy wykorzystać pętlę, aby iteracyjnie dzielić liczbę przez 2, a następnie zapisywać reszty. W tym celu tworzymy zmienną, która będzie przechowywać wynik w postaci ciągu binarnego. Po zakończeniu pętli, odwracamy ciąg, aby uzyskać poprawną reprezentację binarną.
Oto przykładowy kod, który ilustruje ten proces:
def decimal_to_binary(n):
if n == 0:
return "0"
binary = ""
while n > 0:
remainder = n % 2
binary = str(remainder) + binary
n = n // 2
return binary
# Przykład użycia
number = 20
print(f"Liczba {number} w systemie binarnym to: {decimal_to_binary(number)}")
Przykład konwersji liczby w C++: Prosty kod do użycia
W języku C++ konwersja liczby dziesiętnej na system binarny również jest prosta. Możemy użyć pętli do dzielenia liczby przez 2, podobnie jak w Pythonie, ale w tym przypadku musimy użyć tablicy, aby przechować reszty. Po zakończeniu dzielenia, odwracamy tablicę, aby uzyskać binarną reprezentację liczby.
Oto przykład kodu w C++:
#include#include using namespace std; string decimalToBinary(int n) { if (n == 0) return "0"; vector binary; while (n > 0) { binary.push_back(n % 2); n = n / 2; } string result = ""; for (int i = binary.size() - 1; i >= 0; i--) { result += to_string(binary[i]); } return result; } int main() { int number = 20; cout << "Liczba " << number << " w systemie binarnym to: " << decimalToBinary(number) << endl; return 0; }
Jak zamienić liczbę na system binarny w Javie: Krok po kroku
W języku Java konwersja liczby dziesiętnej na system binarny jest również prostym procesem. Możemy użyć pętli, aby dzielić liczbę przez 2, a następnie zapisywać reszty, które tworzą naszą binarną reprezentację. W tym przypadku wykorzystamy zmienną typu String, aby przechować wynik. Po zakończeniu pętli odwracamy ten ciąg, aby uzyskać poprawny format binarny.
Przykładowy kod w Javie, który ilustruje ten proces, wygląda następująco:
public class DecimalToBinary {
public static String decimalToBinary(int n) {
if (n == 0) return "0";
StringBuilder binary = new StringBuilder();
while (n > 0) {
binary.insert(0, n % 2); // Wstawienie reszty na początek
n = n / 2; // Dzielenie przez 2
}
return binary.toString(); // Zwrócenie binarnej reprezentacji
}
public static void main(String[] args) {
int number = 20;
System.out.println("Liczba " + number + " w systemie binarnym to: " + decimalToBinary(number));
}
}
W powyższym kodzie, metoda decimalToBinary przyjmuje liczbę całkowitą jako argument i zwraca jej binarną reprezentację jako String. Używając klasy StringBuilder, możemy efektywnie budować nasz wynik, wstawiając reszty na początku ciągu. W funkcji main testujemy naszą metodę, konwertując liczbę 20 na format binarny, co skutkuje wyświetleniem wyniku na konsoli.
Jak wykorzystać konwersję binarną w praktycznych zastosowaniach
Znajomość konwersji liczb dziesiętnych na system binarny ma wiele praktycznych zastosowań, zwłaszcza w dziedzinie programowania i analizy danych. Przykładowo, w programowaniu niskopoziomowym zrozumienie, jak dane są reprezentowane w systemie binarnym, pozwala programistom na optymalizację kodu oraz lepsze zarządzanie pamięcią. Dzięki konwersji binarnej można również efektywniej manipulować danymi w strukturach takich jak tablice bitowe, które są używane do przechowywania dużych ilości informacji w sposób oszczędzający miejsce.
W kontekście analizy danych, konwersja binarna jest kluczowa w algorytmach kompresji i szyfrowania. Zrozumienie, jak liczby są reprezentowane w systemie binarnym, umożliwia tworzenie bardziej efektywnych algorytmów, które mogą przetwarzać dane w czasie rzeczywistym. W miarę jak technologia rozwija się, umiejętność konwersji i pracy z danymi binarnymi staje się coraz bardziej cenna, zwłaszcza w erze big data i sztucznej inteligencji, gdzie optymalizacja i szybkość przetwarzania danych są kluczowe dla sukcesu projektów.

