Przykłady konwersji i operacji arytmetycznych pomogą Ci lepiej zrozumieć zasady działania tego systemu. Dzięki prostym metodom, które przedstawimy, nauka obliczeń w systemie binarnym stanie się łatwiejsza i bardziej przystępna.
Najważniejsze informacje:
- System binarny używa tylko cyfr 0 i 1 do reprezentowania wartości liczbowych.
- Aby przeliczyć liczbę binarną na dziesiętną, sumuje się wartości potęg liczby 2.
- Konwersja liczby dziesiętnej na binarną polega na dzieleniu przez 2 i zapisywaniu reszt.
- Podstawowe operacje arytmetyczne w systemie binarnym obejmują dodawanie, odejmowanie, mnożenie i dzielenie.
- Dodawanie w systemie binarnym opiera się na prostych zasadach, takich jak przenoszenie.
Jak obliczyć wartość liczby w systemie binarnym – krok po kroku
System binarny jest kluczowym elementem w świecie technologii, ponieważ wszystkie dane w komputerach są reprezentowane w formie binarnej. W tym systemie używamy tylko dwóch cyfr: 0 i 1, co sprawia, że obliczenia stają się bardziej zrozumiałe i precyzyjne. Zrozumienie, jak obliczyć wartość liczby w systemie binarnym, jest niezbędne dla każdego, kto chce zgłębiać temat informatyki i programowania.W artykule przedstawimy, jak przeliczać liczby binarne na dziesiętne oraz odwrotnie, a także jak wykonywać podstawowe operacje arytmetyczne w tym systemie. W miarę postępu w nauce, zauważysz, że obliczenia w systemie binarnym są nie tylko proste, ale również fascynujące, co czyni je niezwykle przydatnymi w codziennym życiu oraz w pracy z technologią.
Jak przeliczyć liczbę binarną na dziesiętną – łatwe metody
Aby przeliczyć liczby binarne na dziesiętne, należy zrozumieć, jak działa system binarny. Każda cyfra w liczbie binarnej ma przypisaną wartość, która jest potęgą liczby 2. Na przykład, w liczbie binarnej 1011, od prawej strony, mamy: 1 (2^0), 1 (2^1), 0 (2^2) oraz 1 (2^3). Obliczając wartość dziesiętną, sumujemy tylko te potęgi, które odpowiadają cyfrom 1. Dlatego 1011 w systemie dziesiętnym to: 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 8 + 0 + 2 + 1 = 11.Proces przeliczania jest prosty i można go wykonać w kilku krokach. Po pierwsze, zapisujemy liczbę binarną i przypisujemy każdej cyfrze odpowiednią potęgę liczby 2. Następnie, dla każdej pozycji, w której znajduje się cyfra 1, dodajemy wartość potęgi do sumy. Na koniec, sumujemy wszystkie wartości, aby uzyskać wynik w systemie dziesiętnym. Dzięki tym prostym krokom, konwersja liczb binarnych na dziesiętne staje się łatwa i zrozumiała.
- Przykład 1: Liczba binarna 1101 to 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 13 w systemie dziesiętnym.
- Przykład 2: Liczba binarna 1001 to 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0 = 9 w systemie dziesiętnym.
- Przykład 3: Liczba binarna 0110 to 0 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 = 6 w systemie dziesiętnym.
| Binary | Decimal |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
Jak konwertować liczbę dziesiętną na binarną – proste kroki
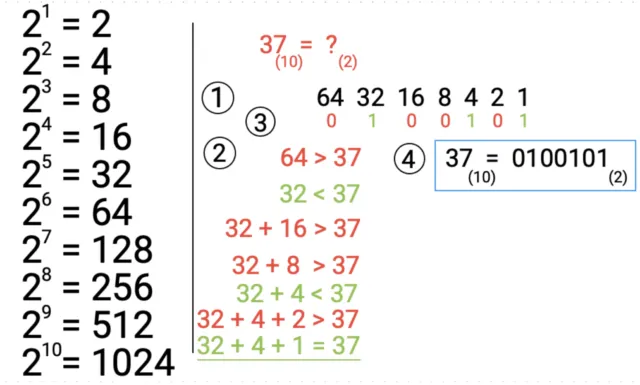
Konwersja liczby dziesiętnej na binarną jest prostym procesem, który można wykonać za pomocą metody dzielenia przez 2. Aby przekształcić liczbę, należy dzielić ją przez 2, zapisując reszty z każdego dzielenia. Przykładowo, przeliczając liczbę 13 na system binarny, zaczynamy od podzielania jej przez 2. 13 podzielone przez 2 daje 6 z resztą 1. Następnie, 6 podzielone przez 2 daje 3 z resztą 0, 3 podzielone przez 2 daje 1 z resztą 1, a 1 podzielone przez 2 daje 0 z resztą 1. Odczytując reszty w odwrotnej kolejności, otrzymujemy liczbę binarną 1101.
Podczas konwersji, kluczowe jest, aby zapisywać każdą resztę z dzielenia, ponieważ to one tworzą wynikową liczbę binarną. Proces ten można podsumować w kilku krokach: dzielimy liczbę przez 2, zapisujemy resztę, powtarzamy ten proces dla wyniku dzielenia, aż do osiągnięcia zera, a następnie odczytujemy reszty w odwrotnej kolejności. Dzięki tej metodzie, każdy może szybko i łatwo przekonwertować liczby dziesiętne na binarne.
| Liczba dziesiętna | Liczba binarna |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
Jak wykonywać podstawowe operacje arytmetyczne w systemie binarnym – zrozumienie zasad
Operacje arytmetyczne w systemie binarnym są kluczowe dla zrozumienia, jak działa komputerowa logika. W przeciwieństwie do systemu dziesiętnego, w którym używamy dziesięciu cyfr, system binarny opiera się wyłącznie na dwóch cyfrach: 0 i 1. Dzięki prostym zasadom dodawania i odejmowania, można łatwo wykonywać obliczenia w tym systemie, co ma ogromne znaczenie w programowaniu i obliczeniach komputerowych.
Dodawanie w systemie binarnym jest bardzo podobne do dodawania w systemie dziesiętnym, ale z mniejszą liczbą zasad. Oto podstawowe zasady: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, a 1 + 1 = 10 (gdzie 0 jest wynikiem, a 1 jest przeniesieniem do następnej pozycji). Na przykład, dodając liczby 1011 i 1101, zaczynamy od prawej strony: 1 + 1 = 10 (przenosimy 1), następnie 1 + 0 + 1 (przeniesienie) = 10 (przenosimy 1), 0 + 1 + 1 (przeniesienie) = 10 (przenosimy 1), a na końcu 1 + 1 = 10, co daje wynik 11010.
Odejmowanie w systemie binarnym również opiera się na prostych zasadach, ale wymaga zrozumienia koncepcji "pożyczki". Główne zasady to: 0 - 0 = 0, 1 - 0 = 1, a 1 - 1 = 0. Jeśli musimy odjąć 1 od 0, musimy "pożyczyć" od sąsiedniej pozycji. Na przykład, aby wykonać odejmowanie 1010 - 0110, zaczynamy od prawej: 0 - 0 = 0, 1 - 1 = 0, 0 - 1 wymaga pożyczki (przekształcamy 10 w 2), więc 10 - 1 = 1. Następnie, 0 - 0 = 0, co daje wynik 0010.
Jak dodawać liczby w systemie binarnym – zasady i przykłady
Dodawanie w systemie binarnym jest prostą, ale ważną operacją, która opiera się na kilku podstawowych zasadach. W tym systemie mamy tylko dwie cyfry: 0 i 1. Oto zasady, które należy zapamiętać: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, a 1 + 1 = 10. Oznacza to, że przy dodawaniu dwóch jedynek, otrzymujemy 0 i przenosimy 1 do następnej pozycji. Na przykład, dodając liczby 1011 i 1101, zaczynamy od prawej: 1 + 1 = 10 (przenosimy 1), następnie 1 + 0 + 1 (przeniesienie) = 10 (przenosimy 1), 0 + 1 + 1 (przeniesienie) = 10 (przenosimy 1), a na końcu 1 + 1 = 10, co daje wynik 11010.
W bardziej złożonym przykładzie, dodajmy liczby 1110 i 1011. Rozpoczynamy od prawej: 0 + 1 = 1, następnie 1 + 1 = 10 (przenosimy 1), 1 + 0 + 1 (przeniesienie) = 10 (przenosimy 1), a na końcu 1 + 1 = 10 (przenosimy 1). Zatem wynik końcowy to 11001. Praktyka w dodawaniu liczb binarnych pozwala na szybkie i efektywne przyswajanie tego systemu, co jest niezwykle przydatne w programowaniu i obliczeniach komputerowych.
Jak odejmować liczby w systemie binarnym – techniki i ilustracje
Odejmowanie w systemie binarnym również opiera się na prostych zasadach, ale wymaga zrozumienia koncepcji "pożyczki". Główne zasady to: 0 - 0 = 0, 1 - 0 = 1, a 1 - 1 = 0. Kiedy musimy odjąć 1 od 0, musimy "pożyczyć" od sąsiedniej pozycji. Na przykład, aby wykonać odejmowanie 1010 - 0110, zaczynamy od prawej: 0 - 0 = 0, 1 - 1 = 0, 0 - 1 wymaga pożyczki, więc przekształcamy 10 w 2, a więc 10 - 1 = 1. Następnie, 0 - 0 = 0, co daje wynik 0010.
W bardziej skomplikowanym przykładzie, rozważmy odejmowanie 1101 - 1010. Rozpoczynamy od prawej: 1 - 0 = 1, następnie 0 - 1 wymaga pożyczki (przekształcamy 10 w 2), więc 10 - 1 = 1. Potem, 0 - 0 = 0, a na końcu 1 - 1 = 0. Zatem wynik końcowy to 0011. Zrozumienie zasad odejmowania w systemie binarnym pomaga uniknąć błędów i ułatwia pracę z bardziej złożonymi obliczeniami.
Czytaj więcej: Jak przelozyc zdanie na system binarny - proste sposoby i narzędzia
Praktyczne zastosowania systemu binarnego w nowoczesnej technologii
System binarny ma kluczowe znaczenie nie tylko w podstawowych obliczeniach, ale także w zaawansowanych technologiach, takich jak programowanie komputerowe, sztuczna inteligencja oraz przetwarzanie danych. Współczesne aplikacje wykorzystują algorytmy oparte na operacjach binarnych do efektywnego zarządzania i przetwarzania informacji. Na przykład, w uczeniu maszynowym, dane są często reprezentowane w formie binarnej, co umożliwia szybsze i bardziej efektywne obliczenia, a także lepsze wykorzystanie pamięci.
Dodatkowo, zrozumienie zasad działania systemu binarnego jest niezbędne w kontekście cyberbezpieczeństwa. Wiele technik szyfrowania opiera się na operacjach binarnych, co sprawia, że znajomość tych zasad pozwala na lepsze zabezpieczanie danych oraz zrozumienie, jak działają różne algorytmy kryptograficzne. W miarę jak technologia rozwija się, umiejętność pracy z systemem binarnym staje się coraz bardziej cenna, otwierając drzwi do innowacyjnych rozwiązań w różnych dziedzinach.