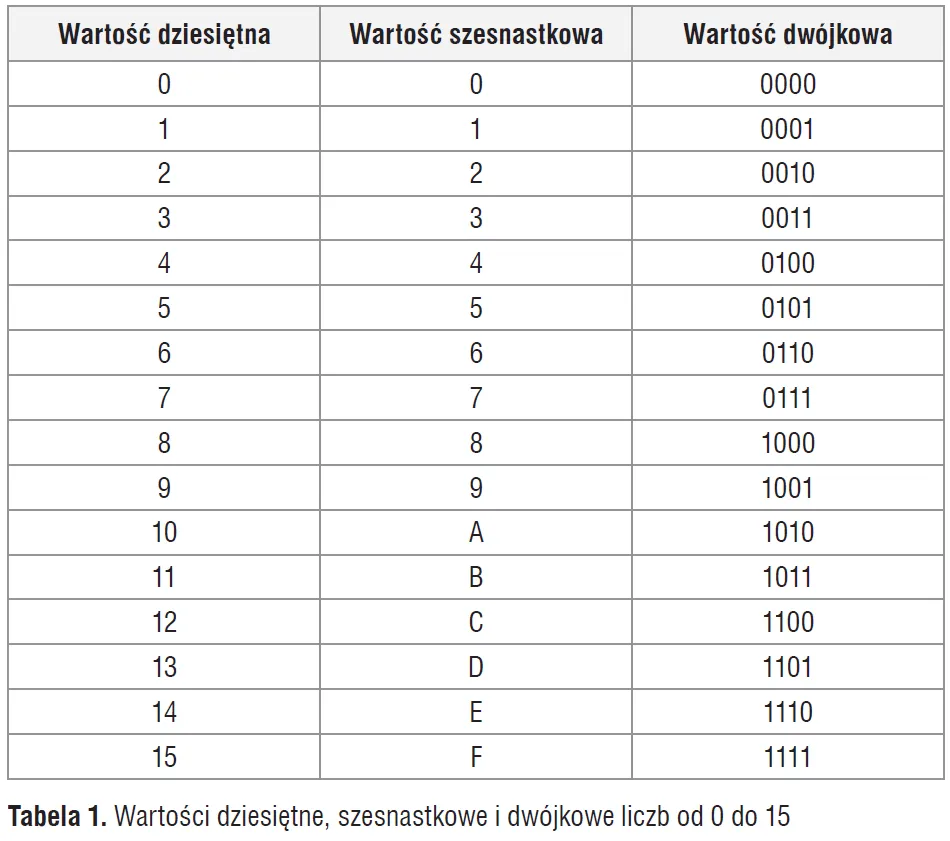
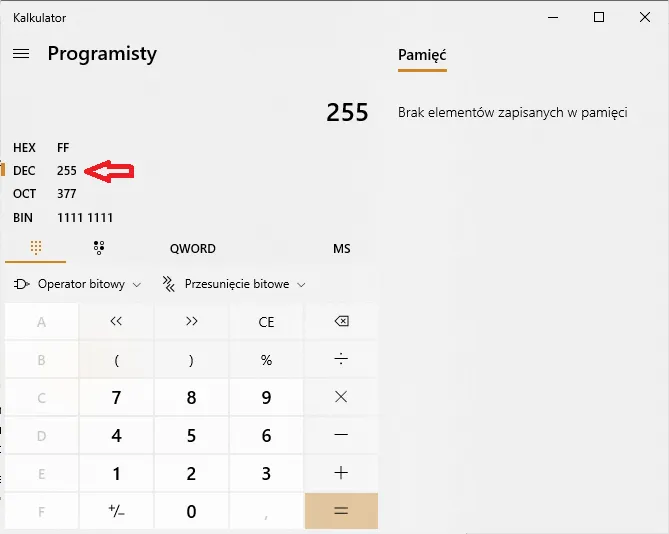
to umiejętność, która staje się coraz bardziej istotna w erze cyfrowej. System binarny, oparty na dwóch cyfrach – 0 i 1 – jest fundamentem działania komputerów i urządzeń elektronicznych. Aby przeliczyć liczbę dziesiętną na binarną, stosuje się prostą metodę dzielenia przez 2, zapisując reszty z dzielenia. W tym artykule przedstawimy krok po kroku, jak przeprowadzić ten proces oraz jak zweryfikować poprawność przeliczenia.
Zrozumienie, jak działa system binarny, nie tylko ułatwia pracę z komputerami, ale także pozwala lepiej pojąć, jak przetwarzane są dane w cyfrowym świecie. W kolejnych częściach artykułu omówimy również, jak konwertować liczby binarne z powrotem na dziesiętne, co pomoże w pełni zrozumieć te kluczowe konwersje.
Kluczowe wnioski:
- Aby przeliczyć liczbę dziesiętną na binarną, należy dzielić ją przez 2 i zapisywać reszty.
- Odczytując reszty od dołu do góry, otrzymujemy reprezentację binarną liczby.
- Konwersja z binarnego na dziesiętny polega na mnożeniu cyfr przez odpowiednie potęgi liczby 2.
- System binarny jest kluczowy dla działania komputerów i urządzeń cyfrowych.
Jak przeliczać liczby dziesiętne na system binarny w prosty sposób
Aby przeliczyć liczbę dziesiętną na system binarny, należy zastosować metodę dzielenia przez 2. Proces ten polega na tym, że dzielimy daną liczbę przez 2, zapisujemy resztę z dzielenia, a następnie dzielimy wynik przez 2 ponownie. Powtarzamy tę czynność, aż do momentu, gdy wynik dzielenia osiągnie 0. Otrzymane reszty, odczytane w odwrotnej kolejności, tworzą reprezentację binarną liczby.
Na przykład, przeliczając liczbę 21, wykonujemy następujące operacje: 21 dzielimy przez 2, co daje 10 z resztą 1. Następnie 10 dzielimy przez 2, co daje 5 z resztą 0, potem 5 dzielimy przez 2, co daje 2 z resztą 1, następnie 2 dzielimy przez 2, co daje 1 z resztą 0, a na końcu 1 dzielimy przez 2, co daje 0 z resztą 1. Odczytując reszty od dołu do góry, uzyskujemy 10101, co oznacza, że 21 w systemie binarnym to 10101₂.
Krok po kroku: Jak dzielić liczby przez 2 dla konwersji
Aby skutecznie przeliczać liczby dziesiętne na binarne, należy postępować według kilku prostych kroków. Po pierwsze, zaczynamy od podzielenia liczby przez 2 i zapisania reszty. Następnie, bierzemy wynik dzielenia i ponownie dzielimy go przez 2, zapisując nową resztę. Kontynuujemy ten proces, aż wynik dzielenia będzie równy 0. Kluczowe jest, aby zapisywać wszystkie reszty, ponieważ będą one potrzebne do utworzenia końcowego wyniku binarnego.
- Podziel liczbę przez 2 i zapisz resztę.
- Weź wynik dzielenia i powtórz proces, aż osiągniesz 0.
- Odczytaj reszty w odwrotnej kolejności, aby uzyskać wynik binarny.
Przykłady konwersji liczb dziesiętnych na binarne
Przyjrzyjmy się kilku konkretnym przykładom, które ilustrują, jak przeliczać liczby dziesiętne na system binarny. Zacznijmy od liczby 10. Dzieląc ją przez 2, otrzymujemy: 10 ÷ 2 = 5 z resztą 0. Następnie 5 dzielimy przez 2, co daje 2 z resztą 1. Kontynuując, 2 dzielimy przez 2, co daje 1 z resztą 0, a na końcu 1 dzielimy przez 2, co daje 0 z resztą 1. Odczytując reszty od dołu do góry, uzyskujemy 1010, co oznacza, że 10₁₀ = 1010₂.
Innym przykładem może być liczba 15. Dzielimy ją przez 2: 15 ÷ 2 = 7 z resztą 1. Następnie 7 ÷ 2 = 3 z resztą 1, potem 3 ÷ 2 = 1 z resztą 1, a na końcu 1 ÷ 2 = 0 z resztą 1. Odczytując reszty, otrzymujemy 1111, co oznacza, że 15₁₀ = 1111₂. Poniższa tabela podsumowuje kilka konwersji liczb dziesiętnych na binarne.
| Liczba dziesiętna | Liczba binarna |
| 10 | 1010 |
| 15 | 1111 |
| 21 | 10101 |
| 30 | 11110 |
| 5 | 101 |
Jak konwertować liczby binarne na dziesiętne bez trudności
Aby przeliczyć liczby binarne na dziesiętne, stosujemy metodę mnożenia. Każda cyfra w liczbie binarnej ma przypisaną wartość, która jest potęgą liczby 2, w zależności od jej pozycji. Zaczynamy od prawej strony, gdzie najniższa cyfra (2⁰) ma wartość 1, następnie przechodzimy do lewej, gdzie każda kolejna cyfra jest mnożona przez 2 podniesione do odpowiedniej potęgi. Na przykład, w liczbie binarnej 1011, ostatnia cyfra (1) jest mnożona przez 2⁰, przedostatnia (1) przez 2¹, następna (0) przez 2², a pierwsza (1) przez 2³.
Po obliczeniu wartości dla każdej cyfry, sumujemy wszystkie wyniki, aby uzyskać wartość dziesiętną. W przypadku liczby 1011, obliczenia będą wyglądać następująco: 1×2³ + 0×2² + 1×2¹ + 1×2⁰ = 8 + 0 + 2 + 1 = 11. Dzięki tej metodzie, można łatwo i szybko przeliczać liczby binarne na dziesiętne, co jest niezwykle przydatne w informatyce i programowaniu.
Zasady mnożenia cyfr binarnych przez potęgi liczby 2
Podczas konwersji z liczb binarnych na dziesiętne, kluczowe jest zrozumienie, jak obliczać wartość każdej cyfry. Każda cyfra binarna reprezentuje potęgę liczby 2, w zależności od jej pozycji. Zaczynając od prawej strony, pierwsza cyfra mnożona jest przez 2⁰, druga przez 2¹, trzecia przez 2², i tak dalej. Na przykład, dla liczby binarnej 1101, obliczenia będą wyglądać następująco: pierwsza cyfra (1) to 1×2⁰, druga cyfra (0) to 0×2¹, trzecia cyfra (1) to 1×2², a czwarta cyfra (1) to 1×2³. Sumując te wartości, uzyskujemy wynik dziesiętny.
Praktyczne przykłady konwersji z binarnego na dziesiętny
Przyjrzyjmy się kilku praktycznym przykładom konwersji liczb binarnych na dziesiętne. Zacznijmy od liczby binarnej 1010. Aby przeliczyć ją na system dziesiętny, stosujemy potęgi liczby 2. Odczytując od prawej do lewej, mamy: 0×2⁰ + 1×2¹ + 0×2² + 1×2³ = 0 + 2 + 0 + 8 = 10. Zatem 1010₂ = 10₁₀. Kolejnym przykładem jest liczba binarna 1101. Tutaj obliczenia wyglądają następująco: 1×2⁰ + 0×2¹ + 1×2² + 1×2³ = 1 + 0 + 4 + 8 = 13. Zatem 1101₂ = 13₁₀.
Warto również rozważyć liczbę binarną 1110. Dla tej liczby obliczenia są następujące: 0×2⁰ + 1×2¹ + 1×2² + 1×2³ = 0 + 2 + 4 + 8 = 14. Ostatecznie 1110₂ = 14₁₀. Poniższa tabela podsumowuje kilka konwersji liczb binarnych na dziesiętne, co może być pomocne w dalszym zrozumieniu tego procesu.
| Liczba binarna | Liczba dziesiętna |
| 1010 | 10 |
| 1101 | 13 |
| 1110 | 14 |
| 1001 | 9 |
| 1111 | 15 |

Dlaczego system binarny jest kluczowy w informatyce
System binarny, oparty na dwóch cyfrach – 0 i 1 – jest fundamentem działania komputerów i urządzeń cyfrowych. Komputery wykorzystują ten system do przechowywania i przetwarzania danych, ponieważ działają na zasadzie włączonego i wyłączonego stanu, co idealnie odpowiada wartościom binarnym. Każda informacja, od tekstu po obrazy, jest konwertowana na ciągi bitów, które są następnie interpretowane przez procesory komputerowe. Dzięki temu, system binarny umożliwia szybkie i efektywne operacje na danych, co jest kluczowe w dzisiejszym świecie technologii.
W kontekście komunikacji cyfrowej, system binarny odgrywa równie ważną rolę. Wszelkie dane przesyłane przez Internet, w tym e-maile, wiadomości i multimedia, są kodowane w formie binarnej. Umożliwia to ich bezstratne przesyłanie oraz łatwe przechowywanie na nośnikach danych. Bez systemu binarnego, współczesna komunikacja cyfrowa, która opiera się na szybkiej wymianie informacji, byłaby niemożliwa. Właśnie dlatego zrozumienie znaczenia systemu binarnego jest kluczowe dla każdego, kto interesuje się informatyką i technologią.
Zrozumienie podstaw działania komputerów i systemów cyfrowych
Komputery działają na zasadzie przetwarzania danych binarnych, co oznacza, że wszystkie operacje są wykonywane w systemie 0 i 1. Każdy bit w liczbie binarnej reprezentuje stan, który może być interpretowany jako włączony (1) lub wyłączony (0). Procesory komputerowe są zaprojektowane do manipulacji tymi bitami, co pozwala na wykonywanie skomplikowanych obliczeń i operacji logicznych. Ponadto, systemy cyfrowe wykorzystują binarne kody do reprezentacji różnych typów danych, takich jak tekst, dźwięk czy obraz, co sprawia, że binarny system jest niezastąpiony w nowoczesnej technologii. Zrozumienie tych podstawowych zasad działania komputerów jest kluczowe dla każdego, kto chce zgłębić temat informatyki i programowania.
Jak wykorzystać system binarny w nowoczesnym programowaniu
W erze cyfrowej, zrozumienie systemu binarnego otwiera drzwi do wielu nowoczesnych technik programowania, takich jak programowanie niskopoziomowe czy algorytmy kompresji danych. Programiści często korzystają z binarnego kodowania, aby optymalizować wydajność aplikacji i efektywnie zarządzać pamięcią. Na przykład, w językach programowania takich jak C czy C++, programiści mogą bezpośrednio manipulować bitami, co pozwala na tworzenie bardziej złożonych struktur danych, takich jak bity flagowe, które mogą reprezentować wiele stanów w jednym bajcie. Poprzez zastosowanie takich technik, można znacząco zwiększyć wydajność aplikacji, co jest kluczowe w zastosowaniach wymagających dużej mocy obliczeniowej.
Dodatkowo, w kontekście sztucznej inteligencji i uczenia maszynowego, zrozumienie binarnych reprezentacji danych jest niezbędne do efektywnego przetwarzania informacji. Na przykład, dane wejściowe dla modeli AI są często kodowane w formacie binarnym, co pozwala na ich szybkie przetwarzanie i analizę. W miarę jak technologia rozwija się, umiejętność pracy z danymi w systemie binarnym stanie się coraz bardziej cenna, umożliwiając programistom i inżynierom tworzenie bardziej zaawansowanych i wydajnych rozwiązań technologicznych.