Kluczowe wnioski:
- System binarny jest podstawowym językiem, w którym komputery przechowują i przetwarzają informacje.
- Składa się z dwóch cyfr: 0 i 1, co czyni go prostym i efektywnym systemem liczbowym.
- Każda cyfra, zwana bitem, reprezentuje wartość zależną od jej pozycji, obliczaną jako suma potęg liczby 2.
- Jest fundamentem działania wszelkich urządzeń cyfrowych i logicznych w elektronice.
- Prostota systemu binarnego umożliwia łatwą implementację sprzętową oraz efektywne przetwarzanie danych.
Zrozumienie systemu binarnego: definicja i podstawowe zasady
System binarny, znany również jako system dwójkowy, to podstawowy system liczbowy, którego fundamentem jest liczba 2. W jego ramach do zapisu liczb wykorzystywane są jedynie dwie cyfry: 0 i 1. Ten system jest kluczowy w świecie technologii cyfrowej, ponieważ to właśnie w nim komputery przechowują i przetwarzają informacje. Dzięki swojej prostocie oraz efektywności, system binarny umożliwia realizację skomplikowanych operacji w sposób zrozumiały dla maszyn.Każda cyfra w liczbie binarnej, nazywana bitem, ma wartość, która zależy od jej pozycji w liczbie. Wartość ta jest obliczana jako suma potęg liczby 2 na poszczególnych pozycjach. Na przykład, w liczbie binarnej 1011, pierwsza cyfra od prawej (1) reprezentuje 2^0, druga (1) to 2^1, trzecia (0) to 2^2, a czwarta (1) to 2^3. Taki sposób reprezentacji danych sprawia, że system binarny jest idealny do przetwarzania informacji w komputerach oraz urządzeniach elektronicznych.
Co to jest system binarny i dlaczego jest ważny?
System binarny jest nie tylko podstawowym językiem dla komputerów, ale również kluczowym elementem nowoczesnej technologii. Jego znaczenie w informatyce jest ogromne, ponieważ wszystkie dane, od tekstu po obrazy, są reprezentowane w formie binarnej. Dzięki temu możliwe jest ich przetwarzanie oraz przechowywanie w pamięci komputerowej. Bez systemu binarnego nie moglibyśmy korzystać z komputerów, smartfonów i innych urządzeń cyfrowych, które są dziś nieodłączną częścią naszego życia.
Jakie są podstawowe elementy systemu binarnego?
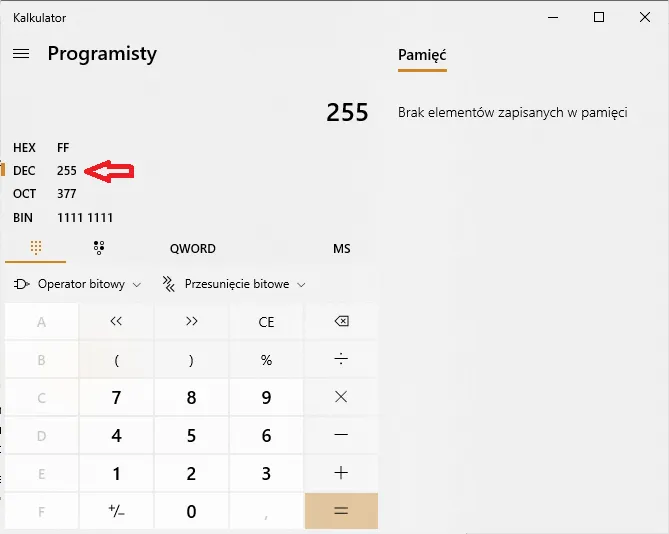
Podstawowymi elementami systemu binarnego są bity i bajty. Bit to najmniejsza jednostka informacji, która może przyjmować jedną z dwóch wartości: 0 lub 1. To właśnie bity stanowią podstawowy język, w którym komputery interpretują i przetwarzają dane. Z kolei bajt składa się z ośmiu bitów i jest używany do reprezentacji bardziej złożonych informacji, takich jak znaki w tekstach czy wartości kolorów w grafice. Dzięki temu, że bajty mogą przechowywać 256 różnych wartości (od 0 do 255), umożliwiają one komputerom efektywne zarządzanie danymi.W systemie binarnym, każdy bit ma swoją specyficzną wartość w zależności od pozycji, na której się znajduje. Na przykład, w liczbie binarnej 1010, pierwszy bit od prawej (0) reprezentuje 2^0, drugi (1) to 2^1, trzeci (0) to 2^2, a czwarty (1) to 2^3. To zrozumienie bitów i bajtów jest kluczowe dla zrozumienia, jak działa system binarny oraz jak jest wykorzystywany w różnych technologiach, takich jak komputery czy urządzenia cyfrowe.
Jak liczby binarne są używane w komputerach?
Liczby binarne odgrywają kluczową rolę w komputerach, ponieważ są podstawowym sposobem reprezentacji danych. Wszelkie informacje, które przetwarzają komputery, takie jak tekst, obrazy czy dźwięki, są konwertowane na format binarny, co umożliwia ich przechowywanie i manipulację. Na przykład, w przypadku plików graficznych, każdy piksel obrazu może być reprezentowany przez zestaw bitów, które określają jego kolor i jasność. Dzięki temu komputery mogą efektywnie zarządzać dużymi zbiorami danych.
Innym przykładem jest pamięć operacyjna, gdzie dane są przechowywane w postaci binarnej. Wysokiej jakości pamięci, takie jak SSD (Solid State Drive), wykorzystują liczby binarne do szybkiego zapisu i odczytu informacji, co znacznie przyspiesza działanie systemów komputerowych. W przeciwieństwie do tradycyjnych dysków twardych HDD (Hard Disk Drive), które mają mechaniczne elementy, SSD działają na zasadzie pamięci flash, co również opiera się na systemie binarnym. Poniższa tabela ilustruje różnice między tymi dwoma metodami przechowywania danych.
| Typ pamięci | Prędkość (odczyt/zapis) | Pojemność | Przykłady |
| SSD | 500 MB/s - 5500 MB/s | 256 GB - 4 TB | Samsung 970 EVO, Crucial MX500 |
| HDD | 80 MB/s - 160 MB/s | 500 GB - 10 TB | Seagate Barracuda, WD Blue |
Przykłady zastosowania systemu binarnego w elektronice
System binarny znajduje szerokie zastosowanie w elektronice, zwłaszcza w urządzeniach codziennego użytku. Na przykład, smartfony wykorzystują liczby binarne do przechowywania danych aplikacji, kontaktów oraz multimediów. Każdy dotyk na ekranie dotykowym jest przetwarzany w postaci sygnałów binarnych, które informują system operacyjny o odpowiednich akcjach. Podobnie, mikrokontrolery w urządzeniach takich jak zdalne piloty czy inteligentne żarówki również operują na danych binarnych, co pozwala im na wykonywanie skomplikowanych zadań przy minimalnym zużyciu energii.
Innym przykładem są telewizory LCD, które wykorzystują system binarny do przetwarzania sygnałów wideo. Obraz jest tworzony z milionów pikseli, z których każdy jest reprezentowany przez liczby binarne. Dzięki temu możliwe jest wyświetlanie wysokiej jakości obrazu oraz dźwięku. Te zastosowania pokazują, jak fundamentalny jest system binarny w nowoczesnej elektronice i jak wpływa na nasze codzienne życie.

Konwersja liczb binarnych: jak działa i dlaczego jest istotna
Konwersja liczb binarnych na system dziesiętny jest procesem, który polega na przekształceniu wartości zapisanej w systemie binarnym (z użyciem cyfr 0 i 1) na odpowiadającą jej wartość w systemie dziesiętnym, który jest bardziej intuicyjny dla ludzi. Aby to zrobić, należy przypisać każdemu bitowi wartość, która jest potęgą liczby 2, w zależności od jego pozycji. Na przykład, w liczbie binarnej 1101, od prawej do lewej, wartości bitów to 2^0, 2^1, 2^2 i 2^3, co daje odpowiednio 1, 2, 0 i 8. Suma tych wartości (1 + 2 + 0 + 8) wynosi 11, co oznacza, że liczba binarna 1101 odpowiada liczbie dziesiętnej 13.
Rozumienie procesu konwersji jest niezwykle ważne, ponieważ umożliwia lepsze zrozumienie, jak dane są przechowywane i przetwarzane przez komputery. Wiedza ta jest kluczowa dla programistów, inżynierów oprogramowania oraz każdego, kto pracuje z systemami komputerowymi. Umiejętność konwersji liczb binarnych na dziesiętne i odwrotnie pozwala na efektywne zarządzanie danymi oraz ich analizę. Ponadto, w kontekście nauki i edukacji, znajomość konwersji wspiera zrozumienie podstawowych zasad działania komputerów i systemów cyfrowych, co jest niezbędne w dzisiejszym zdominowanym przez technologię świecie.
Jak przeliczyć liczby binarne na dziesiętne?
Przeliczenie liczby binarnej na dziesiętną jest procesem, który można zrealizować w kilku prostych krokach. Po pierwsze, należy zidentyfikować pozycje bitów w liczbie binarnej, zaczynając od prawej strony, gdzie pierwszy bit ma wartość 2^0, drugi bit to 2^1, trzeci to 2^2 i tak dalej. Następnie, dla każdego bitu, który ma wartość 1, obliczamy odpowiadającą mu potęgę liczby 2. Na przykład, w liczbie binarnej 1011, mamy: 1×2^3 (8) + 0×2^2 (0) + 1×2^1 (2) + 1×2^0 (1). Suma tych wartości (8 + 0 + 2 + 1) daje wynik 11 w systemie dziesiętnym.
Przykłady konwersji i ich znaczenie w praktyce
Przykłady konwersji liczb binarnych na dziesiętne są nie tylko teoretyczne, ale mają również praktyczne zastosowanie. Na przykład, w programowaniu, często musimy przekształcać liczby binarne, aby zrozumieć, jakie wartości są reprezentowane w pamięci. W przypadku mikrokontrolerów, takich jak Arduino, konwersja binarna jest kluczowa do odczytu wartości czujników i ich interpretacji. W codziennym życiu, konwersja ta jest ważna przy korzystaniu z komputerów, gdzie dane są często zapisywane w formacie binarnym. Zrozumienie tego procesu pozwala na lepsze zarządzanie danymi i ich analizę w różnych aplikacjach.
Przyszłość konwersji binarnych: zastosowanie w AI i uczeniu maszynowym
W miarę jak technologia rozwija się, konwersja liczb binarnych zyskuje na znaczeniu w kontekście sztucznej inteligencji i uczenia maszynowego. W tych dziedzinach, dane są często przetwarzane w formacie binarnym, co umożliwia szybkie i efektywne obliczenia. Zrozumienie, jak przekształcać dane binarne na wartości dziesiętne, jest kluczowe dla programistów, którzy tworzą algorytmy uczące się, ponieważ pozwala to na lepsze modelowanie i analizę danych. Na przykład, w przypadku analizy dużych zbiorów danych, konwersja binarna może być używana do optymalizacji algorytmów, co przyspiesza procesy uczenia i poprawia dokładność wyników.
Co więcej, techniki konwersji binarnej są również wykorzystywane w kompresji danych, co jest niezbędne w dobie ogromnych zbiorów informacji. Zrozumienie, jak działa konwersja, może pomóc w tworzeniu bardziej efektywnych metod kompresji, które zmniejszają rozmiar plików bez utraty jakości. W przyszłości, z rosnącą potrzebą przetwarzania danych w czasie rzeczywistym, umiejętność manipulacji danymi binarnymi stanie się jeszcze bardziej cenna, otwierając nowe możliwości w różnych branżach, od finansów po medycynę.