Przeliczanie liczb z systemu binarnego na dziesiętny to umiejętność, która może wydawać się skomplikowana, ale w rzeczywistości jest dość prosta. W tym artykule przedstawimy, jak łatwo można dokonać tej konwersji, wykorzystując podstawowe zasady matematyczne. Kluczowym krokiem jest zrozumienie, że każda cyfra w liczbie binarnej, zwana bitem, ma swoją wagę, która odpowiada potędze liczby 2, zaczynając od 2^0 dla najbardziej prawej cyfry.
W kolejnych akapitach omówimy krok po kroku proces przeliczania, a także zaprezentujemy konkretne przykłady, które pomogą w zrozumieniu tej tematyki. Zobaczymy, jak przeliczyć zarówno liczby całkowite, jak i te z częścią ułamkową, co pozwoli na pełne opanowanie tej umiejętności.
Najważniejsze informacje:
- Aby przeliczyć liczbę binarną na dziesiętną, każdą cyfrę mnożymy przez odpowiednią potęgę liczby 2.
- Wartość dziesiętna jest sumą wag pozycji, na których znajdują się cyfry 1.
- Przykład konwersji: liczba binarna 101101 odpowiada liczbie dziesiętnej 45.
- W przypadku liczb z częścią ułamkową, stosujemy ujemne potęgi liczby 2 dla cyfr po kropce.
- Konwersję można zrealizować w różnych językach programowania, takich jak Python czy C++.
Jak przeliczyć system binarny na dziesiętny w prostych krokach
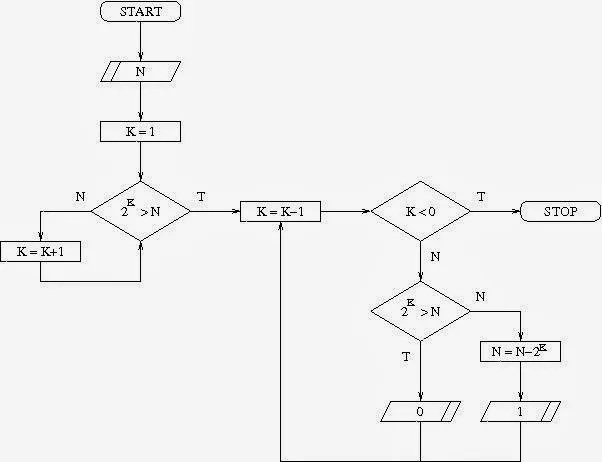
Przeliczanie liczb z systemu binarnego na dziesiętny to kluczowa umiejętność w informatyce i matematyce. System binarny, oparty na dwóch cyfrach – 0 i 1 – jest fundamentem działania komputerów. Każda cyfra w liczbie binarnej, zwana bitem, ma swoją wagę, która odpowiada potędze liczby 2. Zrozumienie tego systemu jest niezbędne do prawidłowego przeliczania wartości binarnych na dziesiętne. Aby przeliczyć liczbę binarną na dziesiętną, należy zastosować prostą metodę. Proces ten polega na pomnożeniu każdej cyfry binarnej przez odpowiednią potęgę liczby 2, zaczynając od potęgi zerowej dla skrajnie prawej cyfry. Następnie, wszystkie uzyskane iloczyny sumuje się, co daje wartość dziesiętną. Kluczowe jest, aby zrozumieć, że tylko cyfry 1 mają znaczenie w tej sumie, ponieważ cyfry 0 nie wnoszą wartości.Zrozumienie podstawowych zasad konwersji binarnej na dziesiętną
System binarny działa na zasadzie dwójkowego kodowania, gdzie każda cyfra (bit) reprezentuje moc liczby 2. Na przykład, pierwsza cyfra z prawej strony ma wartość 2^0, następna 2^1, a kolejna 2^2, i tak dalej. Wartość każdej pozycji w systemie binarnym wzrasta w miarę przesuwania się w lewo. Dlatego ważne jest, aby znać zasady przypisywania wartości poszczególnym cyfrom, co umożliwia poprawne przeliczanie.
- Każda cyfra binarna ma swoją wagę, która odpowiada potędze liczby 2.
- Cyfry 1 w liczbie binarnej mają znaczenie, podczas gdy cyfry 0 nie wpływają na wartość dziesiętną.
- Przy konwersji ważne jest, aby sumować tylko iloczyny cyfr 1 i ich wag.
Krok po kroku: przeliczanie liczb binarnych na dziesiętne
Przeliczanie liczb binarnych na dziesiętne można zrealizować w kilku prostych krokach. Proces ten polega na przyporządkowaniu odpowiednich wag do każdej cyfry w liczbie binarnej, a następnie zsumowaniu wartości tych wag. Niezwykle ważne jest, aby zaczynać od potęgi zerowej dla najbardziej prawej cyfry, a następnie przechodzić w lewo, zwiększając potęgę o jeden. Dzięki temu uzyskamy wartość dziesiętną odpowiadającą danej liczbie binarnej.
Warto pamiętać, że każda cyfra w systemie binarnym ma swoją wagę, która jest równa potędze liczby 2. Na przykład, dla cyfry 1 na pierwszej pozycji z prawej strony, wartość wynosi 2^0, a dla cyfry 1 na drugiej pozycji - 2^1, itd. W ten sposób, po obliczeniu wszystkich wag i ich zsumowaniu, uzyskujemy końcowy wynik.- Rozpocznij od zapisania liczby binarnej, którą chcesz przeliczyć.
- Przypisz każdej cyfrze wagę, zaczynając od potęgi 2^0 dla najbardziej prawej cyfry.
- Mnoż każdą cyfrę binarną przez jej przypisaną wagę.
- Sumuj wszystkie uzyskane iloczyny, aby otrzymać wartość dziesiętną.
Przykłady konwersji liczb binarnych na dziesiętne dla lepszego zrozumienia
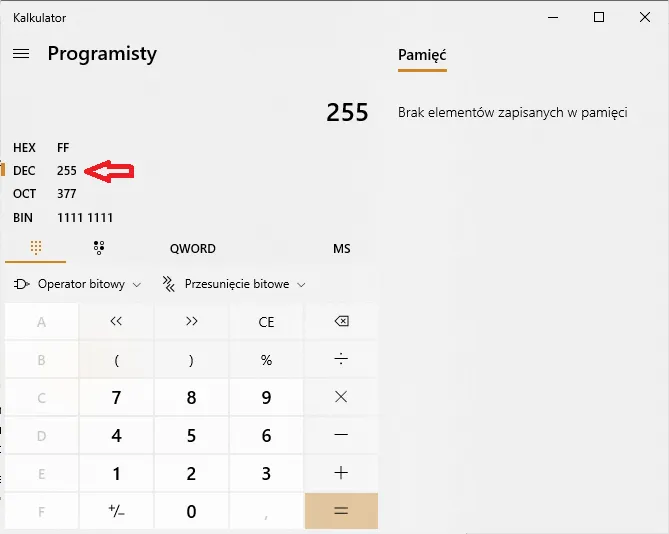
Przykład konwersji liczby binarnej 1010 na system dziesiętny jest doskonałym sposobem na zrozumienie, jak działa przeliczanie systemu binarnego na dziesiętny. Aby to zrobić, musimy przyporządkować odpowiednie wagi każdej cyfrze. Liczba 1010 składa się z dwóch cyfr 1 i dwóch cyfr 0. Rozpoczynamy od najbardziej prawej cyfry, która ma wagę 2^0, następnie przesuwamy się w lewo, gdzie wagi wynoszą odpowiednio 2^1, 2^2 i 2^3. Obliczenia przedstawiają się następująco:1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 8 + 0 + 2 + 0 = 10. W ten sposób, liczba binarna 1010 odpowiada liczbie dziesiętnej 10. To prosty przykład, który ilustruje, jak można z łatwością przeliczać liczby binarne na dziesiętne, stosując zasady konwersji.
Przykład 1: Jak przeliczyć liczbę binarną 1010 na dziesiętną
Aby przeliczyć liczbę binarną 1010 na wartość dziesiętną, wykonujemy następujące obliczenia. Najpierw przypisujemy każdej cyfrze odpowiednią wagę, zaczynając od 2^0 dla najbardziej prawej cyfry. W przypadku liczby 1010, obliczenia wyglądają następująco:
1 \times 2^3 (co daje 8) + 0 \times 2^2 (co daje 0) + 1 \times 2^1 (co daje 2) + 0 \times 2^0 (co daje 0). Po zsumowaniu uzyskujemy: 8 + 0 + 2 + 0 = 10. Tak więc, liczba binarna 1010 odpowiada liczbie dziesiętnej 10.
Przykład 2: Konwersja liczby binarnej 1101 na system dziesiętny
Aby przeliczyć liczbę binarną 1101 na wartość dziesiętną, przeprowadzamy szczegółowe obliczenia, przypisując odpowiednie wagi każdej cyfrze. Liczba 1101 składa się z cyfr 1, 1, 0 oraz 1. Rozpoczynamy proces od przypisania wag, zaczynając od 2^0 dla najbardziej prawej cyfry. W tym przypadku obliczenia wyglądają następująco:
1 × 2^3 (co daje 8) + 1 × 2^2 (co daje 4) + 0 × 2^1 (co daje 0) + 1 × 2^0 (co daje 1). Po zsumowaniu tych wartości otrzymujemy: 8 + 4 + 0 + 1 = 13. Zatem liczba binarna 1101 odpowiada liczbie dziesiętnej 13. To pokazuje, jak prosto można przeliczać liczby binarne na dziesiętne, stosując zasady konwersji.

Jak przeliczać liczby binarne z częścią ułamkową na dziesiętne
Przeliczanie liczb binarnych z częścią ułamkową na system dziesiętny wymaga zrozumienia, jak traktować zarówno część całkowitą, jak i ułamkową. Najpierw konwertujemy część całkowitą, stosując te same zasady, które omówiliśmy wcześniej, przypisując wagę każdej cyfrze binarnej, zaczynając od 2^0 dla najbardziej prawej. Po obliczeniu wartości całkowitej, przechodzimy do części ułamkowej, która wymaga innego podejścia.
Dla części ułamkowej, każda cyfra binarna jest mnożona przez 2 podniesione do ujemnej potęgi, zaczynając od -1 dla pierwszej cyfry po kropce. Na przykład, jeśli mamy liczbę binarną 110.101, część całkowita 110 przelicza się na 6, a część ułamkowa 101 przelicza się na 0.5 + 0 + 0.125, co daje 0.625. Sumując te wartości, otrzymujemy 6.625 jako wartość dziesiętną całej liczby.
Zasady przeliczania części całkowitej i ułamkowej w systemie binarnym
Aby skutecznie przeliczać liczby binarne zawierające zarówno część całkowitą, jak i ułamkową, należy przestrzegać kilku zasad. Część całkowita jest obliczana tak samo jak w przypadku liczb całkowitych, z wagami przypisanymi w standardowy sposób. Z kolei część ułamkowa wymaga, aby każda cyfra była mnożona przez 2 podniesione do ujemnej potęgi, co pozwala na uzyskanie wartości dziesiętnej dla cyfr znajdujących się po kropce. Ważne jest, aby nie mylić tych dwóch procesów, ponieważ obie części mają różne metody przeliczenia.
Praktyczne zastosowania konwersji binarnej w programowaniu i technologii
Znajomość konwersji liczb binarnych na dziesiętne ma kluczowe znaczenie nie tylko dla zrozumienia podstawowych zasad matematyki, ale także dla praktycznych zastosowań w programowaniu i technologii. Wiele języków programowania, takich jak Python, C++ czy Java, pozwala na łatwą konwersję wartości binarnych za pomocą wbudowanych funkcji. Dzięki temu programiści mogą efektywnie przetwarzać dane, które są często reprezentowane w systemie binarnym, np. w kompresji danych, przetwarzaniu obrazów czy analizie sygnałów.
W przyszłości, z rozwojem technologii obliczeniowej i zastosowań sztucznej inteligencji, umiejętność konwersji między systemami liczbowymi stanie się jeszcze bardziej istotna. Na przykład, w kontekście uczenia maszynowego, dane muszą być często przekształcane do formatu, który jest bardziej zrozumiały dla algorytmów. Zrozumienie, jak przeliczać liczby binarne, pozwala programistom na optymalizację algorytmów i efektywniejsze zarządzanie pamięcią, co jest kluczowe w projektach związanych z dużymi zbiorami danych.