Kluczowe informacje:
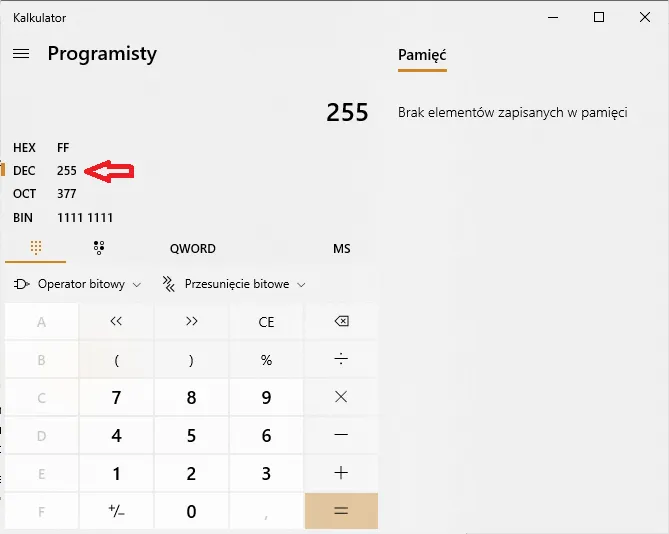
- System binarny oparty jest na dwóch cyfrach: 0 i 1, co czyni go fundamentalnym dla komputerów.
- Każda cyfra w systemie binarnym nazywana jest bitem, a 8 bitów tworzy jeden bajt.
- Komputery wykorzystują stany 0 i 1 do przechowywania i przetwarzania danych, co jest realizowane w układach elektronicznych.
- Konwersja między systemem binarnym a dziesiętnym odbywa się poprzez określone metody, takie jak dzielenie przez 2.
- System binarny ma zastosowanie w różnych urządzeniach elektronicznych, w tym w pamięciach komputerowych i nośnikach danych.
- Istnieje wiele mitów dotyczących działania systemu binarnego, które warto obalić dla lepszego zrozumienia jego funkcji.
Jak działa system binarny i dlaczego jest istotny w technologii?
System binarny, znany także jako system dwójkowy, jest fundamentalnym elementem współczesnych technologii. Oparty na dwóch cyfrach, 0 i 1, stanowi podstawowy język, w którym komputery przechowują i przetwarzają informacje. W historii informatyki, wprowadzenie systemu binarnego zrewolucjonizowało sposób, w jaki dane są przetwarzane, umożliwiając rozwój skomplikowanych systemów komputerowych i urządzeń elektronicznych. Bez systemu binarnego, współczesne technologie, takie jak smartfony, komputery czy internet, nie mogłyby istnieć.Ważność systemu binarnego w nowoczesnym świecie nie może być niedoceniana. Dzięki jego prostocie i niezawodności, komputery mogą efektywnie przetwarzać dane, a także przechowywać je w formie, która jest łatwa do zrozumienia dla urządzeń elektronicznych. System binarny jest również kluczowy dla rozwoju algorytmów i programowania, co sprawia, że zrozumienie jego zasad jest istotne dla każdego, kto chce zgłębiać tajniki technologii.
Zrozumienie podstawowych zasad działania systemu binarnego
System binarny działa na zasadzie reprezentacji danych w postaci bitów i bajtów. Każda cyfra w liczbie binarnej, zwana bitem, może przyjmować jedną z dwóch wartości: 0 lub 1. Osiem bitów tworzy jeden bajt, który jest podstawową jednostką przechowywania danych. W systemie binarnym każda pozycja w liczbie odpowiada potędze liczby 2, co oznacza, że wartość liczby binarnej można obliczyć, sumując wartości odpowiadające poszczególnym bitom.
- Bit to najmniejsza jednostka informacji w systemie binarnym.
- Bajt składa się z 8 bitów i jest używany do przechowywania danych.
- Reprezentacja binarna jest podstawą działania wszystkich urządzeń cyfrowych.
Rola systemu binarnego w przechowywaniu i przetwarzaniu danych
System binarny odgrywa kluczową rolę w przechowywaniu i przetwarzaniu danych w komputerach. Wszystkie informacje, które widzimy na naszych urządzeniach, są ostatecznie reprezentowane w postaci bitów i bajtów. Gdy dane są zapisywane w pamięci, każda cyfra binarna (0 lub 1) jest umieszczana w odpowiedniej pozycji, co pozwala na ich późniejsze odczytanie i przetwarzanie przez procesor. Komputery interpretują te wartości jako stany elektryczne: obecność prądu oznacza 1, a jego brak 0.
Procesor, korzystając z systemu binarnego, wykonuje różne operacje na danych, takie jak dodawanie, odejmowanie czy porównywanie. Każda operacja jest zrealizowana za pomocą logicznych bramek, które działają na zasadzie kombinacji bitów. Dzięki temu, system binarny staje się fundamentem, na którym opiera się cała architektura komputerowa, umożliwiając efektywne przetwarzanie informacji w czasie rzeczywistym.
Metody konwersji między systemem binarnym a dziesiętnym
Konwersja między systemem binarnym a dziesiętnym jest kluczowym procesem, który pozwala na zrozumienie, jak liczby są reprezentowane w różnych systemach liczbowych. Istnieje kilka metod, które umożliwiają tę konwersję. W przypadku konwersji z systemu dziesiętnego na binarny, najpopularniejszą metodą jest wielokrotne dzielenie przez 2, gdzie reszty z dzielenia tworzą reprezentację binarną, odczytywaną od dołu do góry. Na przykład, aby przeliczyć liczbę 10 na system binarny, dzielimy ją przez 2, co daje 5 z resztą 0, następnie 2 z resztą 1, a na końcu 1 z resztą 0. Odczytując reszty, otrzymujemy 1010.
Przy konwersji z systemu binarnego na dziesiętny, każda cyfra binarna jest mnożona przez odpowiednią potęgę liczby 2, a następnie sumowane są wyniki. Na przykład, dla liczby binarnej 1101, obliczamy: 1×2^3 + 1×2^2 + 0×2^1 + 1×2^0, co daje 8 + 4 + 0 + 1 = 13. Dzięki tym metodom, możemy łatwo przechodzić między systemami, co jest niezbędne w programowaniu i informatyce.
- Konwersja dziesiętna na binarną: wielokrotne dzielenie przez 2.
- Konwersja binarna na dziesiętną: suma potęg liczby 2.
- Obie metody są kluczowe dla zrozumienia działania systemu binarnego.
Jak przeliczać liczby dziesiętne na binarne?
Przeliczenie liczby dziesiętnej na system binarny jest procesem, który można przeprowadzić w kilku prostych krokach. Najpierw dzielimy liczbę dziesiętną przez 2, zapisując resztę z dzielenia. Następnie powtarzamy ten proces dla ilorazu, aż do momentu, gdy osiągniemy 0. Po zakończeniu dzielenia, odczytujemy reszty w odwrotnej kolejności, co daje nam reprezentację binarną. Na przykład, aby przeliczyć liczbę 13 na system binarny, dzielimy ją przez 2, co daje 6 z resztą 1, następnie 3 z resztą 0, a na końcu 1 z resztą 1. Odczytując reszty od dołu do góry, otrzymujemy 1101.
Przykłady konwersji binarnej na dziesiętną i odwrotnie
Konwersja między systemami liczbowymi może być ilustrowana za pomocą konkretnych przykładów. Na przykład, liczba binarna 1010 przekształca się na dziesiętną poprzez obliczenie: 1×2^3 + 0×2^2 + 1×2^1 + 0×2^0, co daje 8 + 0 + 2 + 0 = 10. Z kolei liczba dziesiętna 7 przekształca się na binarną poprzez wielokrotne dzielenie przez 2: 7 dzielone przez 2 to 3 z resztą 1, następnie 3 dzielone przez 2 to 1 z resztą 1, a 1 dzielone przez 2 to 0 z resztą 1. Ostatecznie, odczytując reszty, otrzymujemy 111.
| Liczba dziesiętna | Liczba binarna |
| 5 | 101 |
| 10 | 1010 |
| 13 | 1101 |
| 7 | 111 |
Praktyczne zastosowania systemu binarnego w codziennym życiu
System binarny znajduje szerokie zastosowanie w technologii, stanowiąc fundament działania wielu urządzeń, z których korzystamy na co dzień. W komputerach, wszystkie dane, takie jak teksty, obrazy czy dźwięki, są przechowywane w formie binarnej. Dzięki temu, urządzenia mogą szybko i efektywnie przetwarzać informacje. Na przykład, w pamięciach flash, które są powszechnie używane w smartfonach i komputerach, dane są zapisywane jako sekwencje zer i jedynek. To pozwala na szybki dostęp do informacji oraz minimalizację błędów w przechowywaniu danych.
Innym przykładem jest wykorzystanie systemu binarnego w komunikacji sieciowej. Protokół TCP/IP, który jest podstawą działania internetu, operuje na danych w formacie binarnym. Dzięki temu, informacje mogą być przesyłane między różnymi urządzeniami w sposób zrozumiały dla wszystkich systemów. W mikroprocesorach, system binarny umożliwia wykonanie skomplikowanych obliczeń i operacji logicznych, co jest niezbędne do działania zaawansowanych aplikacji i gier komputerowych.
Jak system binarny wpływa na działanie komputerów?
System binarny ma kluczowe znaczenie dla działania komputerów, ponieważ umożliwia im przetwarzanie danych w sposób zrozumiały dla procesorów. Komputery wykonują operacje na danych binarnych za pomocą bramek logicznych, które przetwarzają sygnały elektryczne reprezentujące 0 i 1. Procesor interpretuje te sygnały i wykonuje odpowiednie instrukcje, co pozwala na realizację skomplikowanych zadań, takich jak obliczenia matematyczne czy zarządzanie pamięcią. Dzięki systemowi binarnemu, komputery mogą szybko i efektywnie przetwarzać ogromne ilości informacji, co jest niezbędne w dzisiejszym świecie technologii.
Zastosowania systemu binarnego w urządzeniach elektronicznych
System binarny jest fundamentem działania wielu urządzeń elektronicznych, które wykorzystują go do przechowywania i przetwarzania danych. Na przykład, smartfony używają systemu binarnego do działania aplikacji, przechowywania zdjęć oraz odtwarzania muzyki. W każdym z tych przypadków, dane są kodowane w postaci zer i jedynek, co pozwala na ich szybkie przetwarzanie przez procesory. Kolejnym przykładem są komputery osobiste, które wykorzystują system binarny do realizacji skomplikowanych obliczeń i zarządzania pamięcią. Również telewizory LED operują na danych binarnych, co umożliwia wyświetlanie obrazu i dźwięku w wysokiej jakości.| Urządzenie | Zastosowanie systemu binarnego |
| Smartfon | Przechowywanie danych, działanie aplikacji |
| Komputer osobisty | Obliczenia, zarządzanie pamięcią |
| Telewizor LED | Wyświetlanie obrazu i dźwięku |
| Tablet | Interaktywne aplikacje, multimedia |

Częste błędne przekonania na temat systemu binarnego
Wokół systemu binarnego krąży wiele mitów i nieporozumień, które mogą wprowadzać w błąd. Jednym z najczęstszych przekonań jest to, że system binarny jest zbyt skomplikowany do zrozumienia. W rzeczywistości, jego zasady są stosunkowo proste, opierające się na dwóch wartościach: 0 i 1. Innym mitem jest przekonanie, że system binarny jest używany tylko w komputerach. W rzeczywistości, jest on fundamentem działania wszystkich urządzeń elektronicznych, od telefonów po systemy automatyki domowej. Zrozumienie systemu binarnego jest kluczowe dla każdej osoby, która chce zgłębiać tajniki technologii.
Mity dotyczące działania systemu binarnego w technologii
Istnieje wiele mitów dotyczących działania systemu binarnego, które warto obalić. Na przykład, niektórzy uważają, że system binarny jest mniej wydajny niż systemy dziesiętne. W rzeczywistości, jego prostota sprawia, że jest on bardziej efektywny w kontekście obliczeń komputerowych. Inny mit głosi, że tylko programiści muszą rozumieć system binarny. Jednak każdy użytkownik technologii, od zwykłego konsumenta po inżyniera, powinien mieć podstawową wiedzę na ten temat. Zrozumienie tych kwestii może pomóc w lepszym korzystaniu z nowoczesnych technologii.
Jak system binarny kształtuje przyszłość technologii kwantowej
W miarę jak technologia się rozwija, system binarny zaczyna łączyć się z nowymi koncepcjami, takimi jak komputery kwantowe. W przeciwieństwie do klasycznych komputerów, które operują na bitach, komputery kwantowe wykorzystują qubity, które mogą istnieć w wielu stanach jednocześnie dzięki zasadzie superpozycji. Ta nowa forma przetwarzania danych może zrewolucjonizować sposób, w jaki rozwiązujemy złożone problemy, takie jak kryptografia czy symulacje molekularne. Choć system binarny nadal pozostaje fundamentem klasycznych systemów, jego zasady mogą być adaptowane do działania w kontekście kwantowym, co otwiera drzwi do niespotykanych wcześniej możliwości.
Przykładem zastosowania systemu binarnego w technologii kwantowej jest algorytm Shora, który wykorzystuje qubity do efektywnego łamania klasycznych systemów szyfrowania. Zrozumienie, jak system binarny wpływa na rozwój technologii kwantowej, może pomóc w przygotowaniu się na nadchodzące zmiany w branży technologicznej. Przyszłość technologii z pewnością będzie ściśle związana z ewolucją systemu binarnego, a inwestycja w wiedzę na ten temat może przynieść znaczące korzyści w karierze zawodowej.