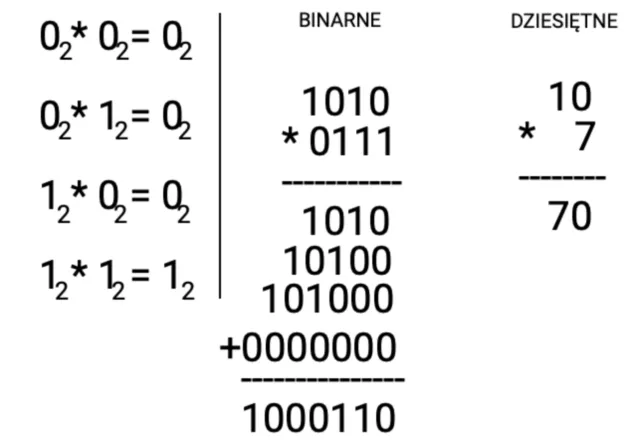
W artykule omówimy również, jak liczby binarne są grupowane w bajty oraz jak można je przekształcać do systemu szesnastkowego dla lepszej czytelności. Zrozumienie tych koncepcji jest kluczowe dla każdego, kto chce zgłębić temat przetwarzania danych w nowoczesnych technologiach.
Najważniejsze informacje:
- System binarny używa tylko dwóch cyfr: 0 i 1.
- Każda cyfra w systemie binarnym to bit, a nie ma potrzeby konwersji binarnej na bity.
- Aby zamienić liczbę dziesiętną na binarną, można użyć metody dzielenia przez 2.
- Przykład konwersji liczby 13 na binarną to 1101.
- Liczby binarne są często grupowane w bajty (8 bitów) dla lepszej organizacji danych.
- Konwersja między systemem binarnym a szesnastkowym jest prosta, ponieważ każda cyfra szesnastkowa odpowiada 4 bitom.
Jak zrozumieć system binarny i jego bity dla lepszej konwersji
System binarny to podstawowy sposób zapisu informacji w informatyce, który wykorzystuje tylko dwie cyfry: 0 i 1. Te cyfry są fundamentem działania komputerów i innych urządzeń elektronicznych. Każda cyfra w systemie binarnym nazywana jest bitem. Dzięki temu, że komputery operują na tych dwóch wartościach, mogą przetwarzać i przechowywać dane w sposób efektywny. W praktyce, zrozumienie systemu binarnego jest kluczowe dla każdego, kto chce zgłębić tajniki informatyki. W systemie binarnym każda wartość liczby jest reprezentowana przez kombinację bitów. Na przykład liczba dziesiętna 5 jest zapisana w systemie binarnym jako 101. To proste przekształcenie pokazuje, jak bity współpracują, aby reprezentować różne wartości. Warto zauważyć, że nie ma potrzeby "konwersji" systemu binarnego na bity, ponieważ bity są jego integralną częścią. Zrozumienie roli bitów jest kluczowe dla dalszego przetwarzania danych oraz konwersji między różnymi systemami liczbowymi.Co to jest system binarny i jak działa w praktyce
System binarny, w przeciwieństwie do systemu dziesiętnego, operuje na dwóch cyfrach: 0 i 1. Historia tego systemu sięga czasów, gdy matematycy zaczęli dostrzegać, że można uprościć obliczenia, ograniczając się do dwóch wartości. Współczesne komputery wykorzystują ten system do przetwarzania danych, co czyni go kluczowym elementem technologii. Dzięki binarnemu systemowi, komputery mogą wykonywać skomplikowane operacje, przechowywać informacje i komunikować się ze sobą.
- System binarny jest podstawą działania wszystkich nowoczesnych komputerów.
- Każda cyfra w systemie binarnym to bit, co czyni go fundamentalnym elementem zapisu danych.
- Przykład liczby 5 w systemie binarnym to 101, co ilustruje, jak bity mogą reprezentować różne wartości.
| Liczba dziesiętna | Liczba binarna |
| 2 | 10 |
| 5 | 101 |
| 10 | 1010 |
Jakie są bity i ich rola w systemie binarnym
Bity to najmniejsze jednostki informacji w systemie binarnym, które mogą przyjmować jedną z dwóch wartości: 0 lub 1. Każdy bit jest kluczowym elementem w reprezentacji danych, ponieważ to właśnie kombinacje tych dwóch wartości pozwalają na zapisanie wszelkich informacji w komputerze. W praktyce, bity są używane do kodowania tekstu, obrazów, dźwięku i innych typów danych, co czyni je fundamentalnym składnikiem technologii informacyjnej.
W systemie binarnym, każdy bit ma swoją specyficzną pozycję, co wpływa na jego wartość. Na przykład, w liczbie binarnej 101, pierwszy bit (od prawej) ma wartość 1, drugi bit wartość 0, a trzeci bit wartość 4. Dzięki temu, bity współpracują ze sobą, tworząc liczby binarne, które są następnie przetwarzane przez komputery. Bez bitów, nie byłoby możliwe przechowywanie ani przetwarzanie informacji w sposób, do którego jesteśmy przyzwyczajeni.
- Bity są podstawowymi jednostkami danych w systemie binarnym.
- Każdy bit może przyjmować wartość 0 lub 1, co pozwala na kodowanie różnych informacji.
- Kombinacje bitów tworzą liczby binarne, które są kluczowe dla działania komputerów.
| Bit | Wartość |
| 0 | Brak informacji |
| 1 | Obecność informacji |
Krok po kroku: Przykład konwersji liczby dziesiętnej
Aby zamienić liczbę dziesiętną na system binarny, możemy użyć metody dzielenia przez 2. Weźmy na przykład liczbę 13. Pierwszym krokiem jest podzielenie 13 przez 2, co daje 6, a reszta to 1. Następnie dzielimy 6 przez 2, co daje 3, a reszta to 0. Kolejny krok to dzielenie 3 przez 2, co daje 1, a reszta to 1. Na koniec dzielimy 1 przez 2, co daje 0, a reszta to 1. Teraz, aby uzyskać wynik w systemie binarnym, czytamy reszty od dołu do góry: 1101. Tak więc, liczba 13 w systemie dziesiętnym to 1101 w systemie binarnym.
Alternatywne metody konwersji: Inne podejścia do przeliczeń
Oprócz metody dzielenia przez 2, istnieją również inne sposoby konwersji liczb dziesiętnych na binarne. Jednym z nich jest użycie algorytmu, który wykorzystuje potęgi liczby 2 do określenia, które bity powinny być ustawione na 1. Można również skorzystać z narzędzi online, które automatycznie dokonują konwersji. Wizualne reprezentacje, takie jak diagramy, mogą pomóc w zrozumieniu procesu konwersji. Dzięki tym różnym metodom, każdy może łatwo przekształcić liczby dziesiętne w ich odpowiedniki binarne.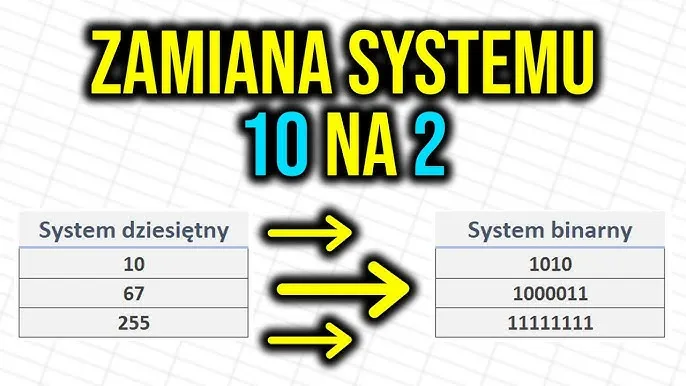
Jak grupować bity w bajty dla lepszej czytelności danych
Bajt to jednostka informacji składająca się z 8 bitów. Jest to podstawowa jednostka danych w informatyce, która pozwala na efektywne przechowywanie i przetwarzanie informacji. Dzięki grupowaniu bitów w bajty, komputer może łatwiej zarządzać danymi, co jest kluczowe w kontekście zarówno pamięci, jak i transferu informacji. Bajty są używane do reprezentacji różnych typów danych, takich jak znaki tekstowe czy wartości liczbowych, co sprawia, że są niezwykle istotne w programowaniu i projektowaniu systemów informatycznych.
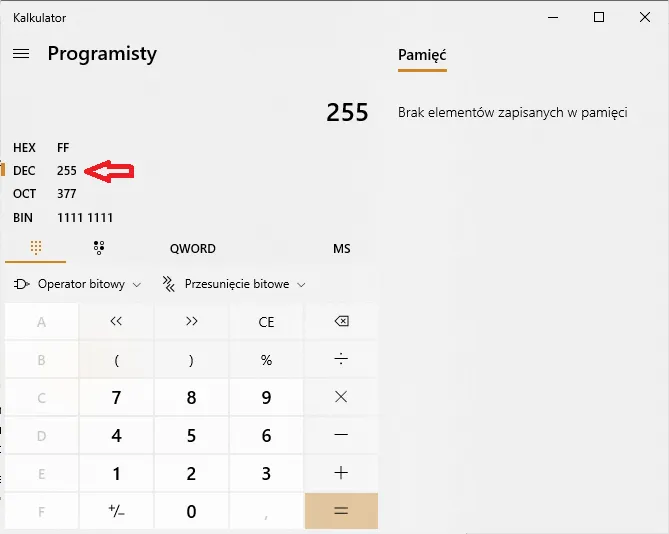
Grupowanie bitów w bajty pozwala na lepszą organizację danych. Każdy bajt może reprezentować 256 różnych wartości (od 0 do 255), co jest wystarczające do zakodowania większości znaków w standardzie ASCII. Dzięki temu, że bity są zgrupowane w bajty, programiści mogą łatwiej operować na danych, a komputery mogą efektywniej je przetwarzać. W praktyce, liczby binarne są często wyrażane w postaci bajtów, co ułatwia ich interpretację i manipulację w aplikacjach komputerowych.
Co to jest bajt i dlaczego jest istotny w informatyce
Bajt to jednostka danych, która składa się z 8 bitów. Jest to standardowa jednostka używana do reprezentacji informacji w komputerach. Bajty są kluczowe, ponieważ umożliwiają przechowywanie i przetwarzanie danych w sposób zorganizowany i efektywny. W informatyce, bajty są często używane do kodowania tekstu, obrazów oraz dźwięku, co czyni je niezbędnymi w codziennym użytkowaniu technologii.
- Bajt składa się z 8 bitów, co pozwala na reprezentację 256 różnych wartości.
- Bajty są podstawową jednostką danych w informatyce, co czyni je kluczowymi w programowaniu.
- W praktyce, bajty są używane do kodowania różnych typów informacji, takich jak tekst, obrazy czy dźwięk.
| Typ danych | Reprezentacja w bajtach |
| Tekst (ASCII) | 1 bajt |
| Obraz (JPEG) | Wiele bajtów |
| Dźwięk (MP3) | Wiele bajtów |
Jak konwertować między systemem binarnym a szesnastkowym
Konwersja między systemem binarnym a szesnastkowym jest stosunkowo prosta, ponieważ każda cyfra szesnastkowa odpowiada dokładnie 4 bitom. Aby przekonwertować liczbę binarną na szesnastkową, należy podzielić ciąg bitów na grupy po 4 bity, zaczynając od prawej. Na przykład, liczba binarna 11010110 dzieli się na grupy: 1101 i 0110. Następnie każdą grupę przekształcamy w odpowiadającą cyfrę szesnastkową: 1101 to D, a 0110 to 6, co daje wynik D6. Z drugiej strony, aby przekształcić liczbę szesnastkową na binarną, każdą cyfrę szesnastkową zamieniamy na jej odpowiednik binarny, na przykład 2 to 0010, a 9 to 1001.
| Liczba szesnastkowa | Liczba binarna |
| 0 | 0000 |
| 1 | 0001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Jak wykorzystać systemy binarne i szesnastkowe w programowaniu
Wykorzystanie systemów binarnych i szesnastkowych w programowaniu ma kluczowe znaczenie dla efektywności i optymalizacji kodu. Programiści często korzystają z tych systemów do tworzenia algorytmów, które operują na danych w sposób zrozumiały dla komputerów. Na przykład, w językach programowania takich jak C czy Python, konwersja między tymi systemami może być używana do manipulacji danymi na poziomie bitów, co pozwala na tworzenie bardziej wydajnych aplikacji. Dzięki temu programiści mogą efektywnie zarządzać pamięcią i szybkością przetwarzania danych.
W przyszłości, z rozwojem technologii takich jak uczenie maszynowe i analiza danych, umiejętność pracy z różnymi systemami liczbowymi stanie się jeszcze bardziej istotna. W miarę jak dane stają się coraz bardziej złożone, programiści będą musieli wykorzystywać zaawansowane techniki konwersji oraz reprezentacji danych, aby zoptymalizować swoje aplikacje. Zrozumienie, jak działa konwersja między systemem binarnym a szesnastkowym, może otworzyć drzwi do tworzenia bardziej zaawansowanych i innowacyjnych rozwiązań technologicznych.