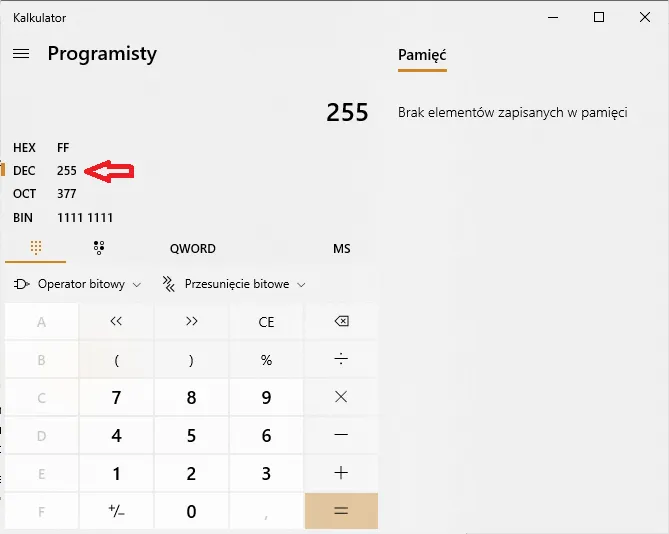
Konwersja może być wykonana ręcznie lub przy użyciu prostych algorytmów w popularnych językach programowania, takich jak Python, C++ czy Java. W artykule przedstawimy zarówno manualne metody przeliczeń, jak i przykłady kodu, które ułatwią automatyzację tego procesu. Dzięki temu, nawet osoby bez zaawansowanej wiedzy technicznej będą mogły zrozumieć, jak zmienić system binarny na dziesiętny.
Najistotniejsze informacje:
- Aby zamienić liczbę binarną na dziesiętną, należy zsumować wartości potęg liczby 2 dla cyfr 1.
- Przykład: liczba binarna 1101 to 13 w systemie dziesiętnym.
- Można użyć funkcji wbudowanych w językach programowania, takich jak `int()` w Pythonie.
- W C++ można iterować przez cyfry liczby binarnej, aby obliczyć wynik.
- Java oferuje metodę `Integer.parseInt(binaryString, 2)` do szybkiej konwersji.
- Ręczne algorytmy również są dostępne dla tych, którzy preferują tradycyjne podejście.
Jak zrozumieć konwersję z systemu binarnego na dziesiętny i jej znaczenie
Konwersja z systemu binarnego na dziesiętny jest kluczowym procesem w informatyce, który umożliwia zrozumienie, jak komputery interpretują dane. System binarny, oparty na dwóch cyfrach (0 i 1), jest podstawą działania wszystkich urządzeń cyfrowych. Z kolei system dziesiętny, którym posługujemy się na co dzień, składa się z dziesięciu cyfr (od 0 do 9). Zrozumienie różnic między tymi dwoma systemami jest niezbędne, aby móc skutecznie przekształcać liczby i analizować dane w różnych kontekstach. Warto zauważyć, że każda cyfra w systemie binarnym ma przypisaną wartość potęgi liczby 2, co czyni go wyjątkowym w porównaniu do systemu dziesiętnego. Na przykład, liczba binarna 1101 w systemie dziesiętnym odpowiada liczbie 13. Zrozumienie tego procesu jest nie tylko istotne dla programistów, ale również dla każdego, kto chce lepiej zrozumieć, jak działają nowoczesne technologie.Co to jest system binarny i dziesiętny oraz ich różnice
System binarny to system liczbowy, który wykorzystuje tylko dwie cyfry: 0 i 1. Każda cyfra w tym systemie reprezentuje potęgę liczby 2, co pozwala na efektywne przechowywanie i przetwarzanie informacji w komputerach. Natomiast system dziesiętny, którym posługujemy się na co dzień, opiera się na dziesięciu cyfrach i jest bardziej intuicyjny dla ludzi.Główna różnica między tymi systemami polega na sposobie, w jaki liczby są reprezentowane. W systemie binarnym każda cyfra ma znaczenie w kontekście potęg liczby 2, co sprawia, że konwersja do systemu dziesiętnego wymaga zrozumienia tych wartości. Dzięki temu różne urządzenia cyfrowe mogą efektywnie komunikować się i przetwarzać dane w sposób, który jest zrozumiały dla użytkowników.
Dlaczego warto znać konwersję między systemami liczbowymi
Znajomość konwersji między systemami liczbowymi, zwłaszcza binarnym i dziesiętnym, jest niezwykle ważna w dzisiejszym świecie technologicznym. Umiejętność ta pozwala nie tylko na lepsze zrozumienie działania komputerów, ale także na skuteczniejsze rozwiązywanie problemów związanych z programowaniem i analizą danych. W różnych dziedzinach, takich jak inżynieria, informatyka czy nauki ścisłe, konwersja ta jest niezbędna.
- Programiści muszą często przekształcać liczby binarne na dziesiętne, aby zrozumieć działanie algorytmów.
- W elektronice, znajomość tych systemów jest kluczowa przy projektowaniu układów cyfrowych.
- W naukach komputerowych konwersja ta pomaga w analizie danych i tworzeniu efektywnych rozwiązań.
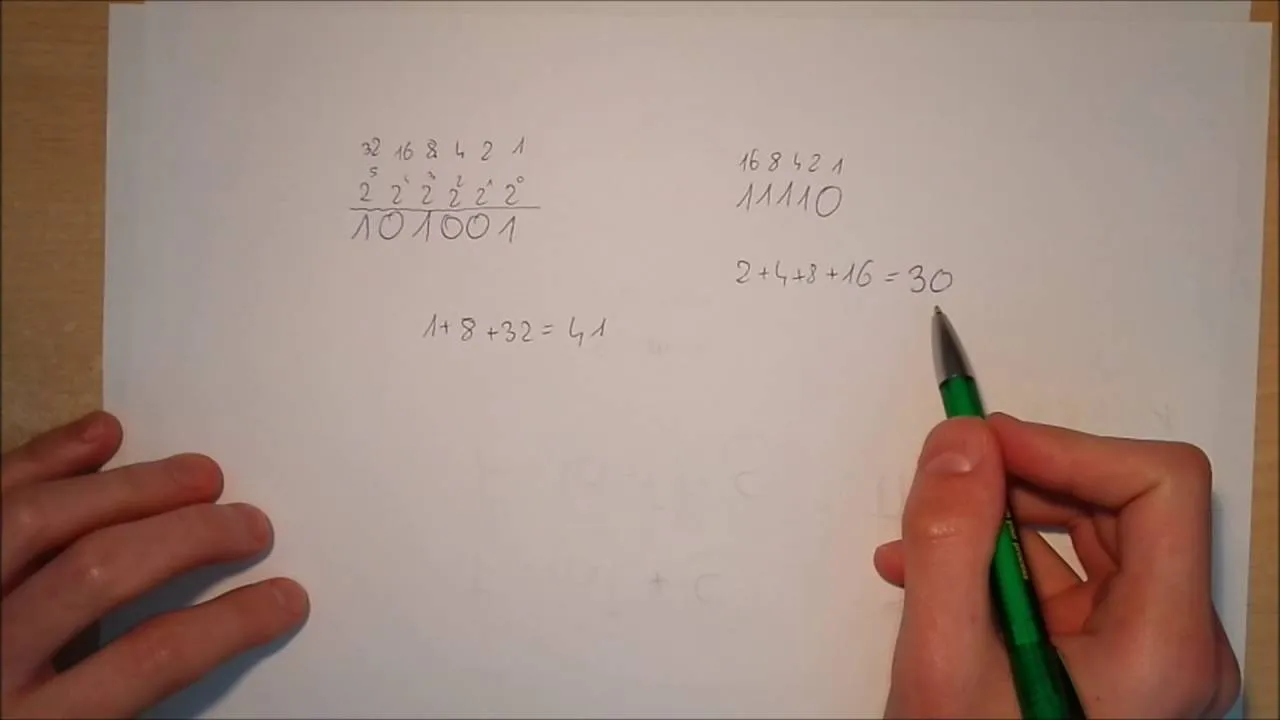
Proste metody konwersji liczby binarnej na dziesiętną
Konwersja liczby binarnej na dziesiętną to proces, który można wykonać ręcznie, korzystając z prostych metod. Aby to zrobić, należy zrozumieć, jak działają potęgi liczby 2. Każda cyfra w liczbie binarnej ma przypisaną wartość, która jest potęgą liczby 2, zaczynając od prawej strony, gdzie potęga zerowa oznacza wartość 1. Wartości cyfr 1 są sumowane, co pozwala uzyskać wynik w systemie dziesiętnym. W ten sposób można łatwo przeliczyć dowolną liczbę binarną na jej odpowiednik dziesiętny.
Przykładowo, dla liczby binarnej 1011, obliczenia wyglądają następująco: 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0, co daje 8 + 0 + 2 + 1, a w rezultacie 11 w systemie dziesiętnym. Taka metoda jest bardzo przydatna, gdy nie mamy dostępu do narzędzi programistycznych i musimy wykonać konwersję ręcznie.
Krok po kroku: Jak przeliczyć liczbę binarną ręcznie
Aby przeliczyć liczbę binarną ręcznie, należy postępować zgodnie z kilkoma prostymi krokami. Po pierwsze, zapisz liczbę binarną, a następnie przypisz każdej cyfrze wartość potęgi liczby 2, zaczynając od prawej. Następnie, dla każdej cyfry 1, oblicz odpowiednią potęgę i zsumuj wyniki. Warto pamiętać, że cyfry 0 nie wpływają na końcowy wynik, więc można je zignorować w obliczeniach.
Na przykład, przeliczając liczbę binarną 1101, wykonujemy następujące obliczenia: 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0. To daje nam 8 + 4 + 0 + 1, co łącznie daje 13 w systemie dziesiętnym. Taki sposób konwersji jest prosty i efektywny, idealny dla osób, które chcą zrozumieć, jak działa ten proces.
Przykłady konwersji binarnych na dziesiętne dla lepszego zrozumienia
Aby lepiej zrozumieć, jak działa konwersja z systemu binarnego na dziesiętny, warto przyjrzeć się kilku konkretnym przykładom. Te przykłady ilustrują, jak liczby binarne są przekształcane w ich odpowiedniki dziesiętne, co może być pomocne w praktycznych zastosowaniach. Poniżej znajduje się tabela z wybranymi liczbami binarnymi i ich wartościami w systemie dziesiętnym.
| Liczba binarna | Liczba dziesiętna |
| 1010 | 10 |
| 1111 | 15 |
| 1001 | 9 |
Przykłady kodu w Pythonie do konwersji binarnej na dziesiętną
W Pythonie konwersja z systemu binarnego na dziesiętny jest bardzo prosta dzięki wbudowanej funkcji `int()`. Ta funkcja pozwala na łatwe przekształcenie liczby binarnej w formacie tekstowym na jej odpowiednik dziesiętny. Wystarczy podać ciąg binarny oraz podstawę, która w tym przypadku wynosi 2. Dzięki temu programiści mogą szybko i efektywnie przeprowadzać konwersje bez potrzeby implementowania skomplikowanych algorytmów.
Oto przykład kodu, który ilustruje, jak używać funkcji `int()` do konwersji liczby binarnej na dziesiętną:
binary_number = "1101" decimal_number = int(binary_number, 2) print(decimal_number) # Wynik to 13
W powyższym przykładzie, liczba binarna "1101" jest przekazywana do funkcji `int()`, która zwraca wartość 13 w systemie dziesiętnym. Taki sposób konwersji jest szybki i wygodny, idealny dla programistów pracujących z danymi binarnymi.
Jak używać C++ do konwersji systemu binarnego na dziesiętny
W języku C++ konwersja z systemu binarnego na dziesiętny można zrealizować poprzez iterację po cyfrach liczby binarnej. Programista może zacząć od końca ciągu binarnego, obliczając wartość potęg liczby 2 dla każdej cyfry 1. W ten sposób można zbudować odpowiednią wartość dziesiętną, sumując wyniki dla każdej cyfry. Poniżej przedstawiamy prosty przykład kodu, który ilustruje ten proces.
Oto przykład kodu w C++:
#include#include #include int binaryToDecimal(const std::string &binary) { int decimal = 0; int length = binary.length(); for (int i = 0; i < length; ++i) { if (binary[length - 1 - i] == '1') { decimal += pow(2, i); } } return decimal; } int main() { std::string binary_number = "1101"; int decimal_number = binaryToDecimal(binary_number); std::cout << decimal_number; // Wynik to 13 return 0; }
W tym przykładzie funkcja `binaryToDecimal` przyjmuje ciąg binarny jako argument i oblicza jego wartość dziesiętną. Działa to poprzez iterację od końca ciągu, dodając odpowiednie potęgi liczby 2 dla każdej cyfry 1. W rezultacie, dla liczby binarnej "1101", program zwraca wartość 13 w systemie dziesiętnym.
Metody konwersji w Javie: Szybkie i efektywne rozwiązania
W języku Java konwersja z systemu binarnego na dziesiętny jest również prosta i efektywna dzięki wbudowanym metodom. Najczęściej używaną metodą jest `Integer.parseInt()`, która pozwala na szybkie przekształcenie ciągu binarnego w jego odpowiednik dziesiętny. Wystarczy podać odpowiedni ciąg binarny oraz podstawę (w tym przypadku 2), aby uzyskać wynik w systemie dziesiętnym. Dzięki tej metodzie programiści mogą szybko implementować konwersję w swoich aplikacjach.
Oto przykład kodu w Javie, który ilustruje, jak używać metody `Integer.parseInt()` do konwersji liczby binarnej:
public class BinaryToDecimal {
public static void main(String[] args) {
String binaryNumber = "1101";
int decimalNumber = Integer.parseInt(binaryNumber, 2);
System.out.println(decimalNumber); // Wynik to 13
}
}
W tym przykładzie, ciąg binarny "1101" jest przekazywany do metody `Integer.parseInt()`, która zwraca wartość 13 w systemie dziesiętnym. Jest to szybki sposób na konwersję, który eliminuje potrzebę manualnych obliczeń, co czyni go idealnym rozwiązaniem dla programistów pracujących z danymi binarnymi.
Jak wykorzystać konwersję binarną w projektach informatycznych
Znajomość konwersji z systemu binarnego na dziesiętny ma wiele praktycznych zastosowań w różnych projektach informatycznych. Na przykład, w tworzeniu gier komputerowych, programiści mogą wykorzystać konwersję binarną do zarządzania stanami gry, gdzie liczby binarne mogą reprezentować różne stany obiektów w grze, takie jak zdrowie, poziom energii czy status misji. Dzięki temu, umiejętność przekształcania tych wartości na system dziesiętny umożliwia łatwiejsze debugowanie i optymalizację kodu.
W przyszłości, z rozwojem technologii takich jak Internet Rzeczy (IoT), konwersja binarna zyska jeszcze większe znaczenie. W urządzeniach IoT, gdzie dane są często przesyłane w formacie binarnym, umiejętność szybkiej konwersji na system dziesiętny pozwoli na efektywniejsze przetwarzanie i analizę danych w czasie rzeczywistym. Dlatego warto rozwijać te umiejętności, aby być gotowym na nadchodzące wyzwania w dziedzinie technologii.