Jak się liczy system binarny - proste metody i przykłady obliczeń

System binarny to podstawowy sposób reprezentacji danych w komputerach, oparty na dwóch cyfrach: 0 i 1. W przeciwieństwie do systemu dziesiętnego, który używa dziesięciu cyfr, system binarny wykorzystuje jedynie dwie, co czyni go idealnym dla technologii cyfrowych. Każda cyfra w liczbie binarnej odpowiada potędze liczby 2, co pozwala na łatwe przeliczanie na wartości dziesiętne oraz odwrotnie. W tym artykule przedstawimy proste metody obliczeń w systemie binarnym oraz przykłady, które pomogą zrozumieć, jak działa ten system. Znajomość systemu binarnego jest niezbędna dla każdego, kto chce zrozumieć podstawy informatyki i działania urządzeń cyfrowych. Dzięki tej wiedzy można łatwo przeliczać liczby oraz wykonywać podstawowe operacje arytmetyczne, które są fundamentem działania komputerów i innych urządzeń elektronicznych.

Najistotniejsze informacje:

• System binarny używa tylko dwóch cyfr: 0 i 1.
• Każda cyfra w systemie binarnym odpowiada potędze liczby 2.
• Konwersja z systemu binarnego na dziesiętny polega na sumowaniu iloczynów cyfr i ich wag.
• Przykład: liczba binarna 101101 odpowiada liczbie dziesiętnej 45.
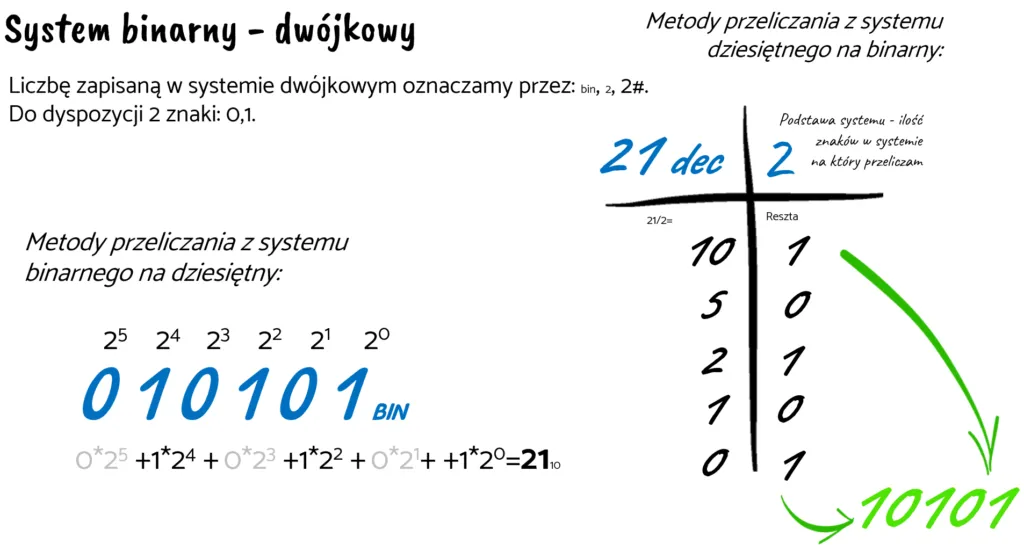
• Aby przeliczyć liczbę dziesiętną na binarną, dzielimy ją przez 2 i zapisujemy reszty w odwrotnej kolejności.
• System binarny jest fundamentem działania komputerów, odpowiadając stanom włączony/wyłączony.

Jak działa system binarny i dlaczego jest ważny w obliczeniach

System binarny, znany również jako system dwójkowy, jest podstawowym sposobem reprezentacji danych w informatyce. W tym systemie używane są tylko dwie cyfry: 0 i 1, co odzwierciedla stany włączony i wyłączony. Każda cyfra w liczbie binarnej odpowiada potędze liczby 2, co sprawia, że system ten jest niezwykle efektywny w obliczeniach komputerowych. Jego prostota i jednoznaczność pozwalają na łatwe przetwarzanie informacji przez urządzenia elektroniczne.

W kontekście obliczeń, system binarny jest kluczowy, ponieważ stanowi fundament działania komputerów. Dzięki jego zastosowaniu, urządzenia mogą wykonywać skomplikowane operacje matematyczne oraz przechowywać i przetwarzać dane w sposób efektywny. Bez systemu binarnego rozwój technologii cyfrowej, w tym komputerów, smartfonów i innych urządzeń, byłby niemożliwy.

Zrozumienie podstaw systemu binarnego i jego zastosowań

Podstawy systemu binarnego opierają się na reprezentacji danych za pomocą dwóch cyfr. Każda pozycja w liczbie binarnej ma przypisaną wagę, która jest potęgą liczby 2. Na przykład, w liczbie binarnej 1011, od prawej strony, cyfry mają wartości: 1 (2⁰), 1 (2¹), 0 (2²), 1 (2³). Takie podejście umożliwia komputerom przechowywanie i przetwarzanie informacji w sposób zrozumiały dla maszyn.

System binarny znajduje zastosowanie w wielu dziedzinach, od programowania po telekomunikację. W informatyce, liczby binarne są używane do kodowania danych, co pozwala na ich efektywne przesyłanie i przechowywanie. Każde urządzenie cyfrowe, takie jak komputery, telefony komórkowe czy urządzenia IoT, opiera swoje działanie na zasadach systemu binarnego, co czyni go kluczowym elementem nowoczesnej technologii.

Jak przeliczać liczby binarne na dziesiętne w prosty sposób

Przeliczanie liczb binarnych na dziesiętne jest kluczową umiejętnością w pracy z systemem binarnym. Proces ten polega na zrozumieniu, jak każda cyfra w liczbie binarnej odpowiada potędze liczby 2. Aby przeliczyć liczbę binarną, należy pomnożyć każdą cyfrę przez wagę jej pozycji, a następnie zsumować wszystkie uzyskane wartości. Dzięki temu możemy łatwo uzyskać wartość dziesiętną z liczby zapisanej w systemie binarnym. Na przykład, aby przeliczyć liczbę binarną 1101 na system dziesiętny, zaczynamy od prawej strony. Każda cyfra jest mnożona przez odpowiednią potęgę liczby 2: 1 (2⁰), 0 (2¹), 1 (2²), 1 (2³). Następnie sumujemy te wartości: 1 + 0 + 4 + 8 = 13. W ten sposób uzyskujemy, że liczba binarna 1101 odpowiada liczbie dziesiętnej 13.

Aby ułatwić przeliczenie liczby binarnej na dziesiętną, można skorzystać z poniższej listy kroków:

• 1. Zapisz liczbę binarną, którą chcesz przeliczyć.
• 2. Przypisz każdej cyfrze wagę odpowiadającą potędze liczby 2, zaczynając od prawej strony (2⁰, 2¹, 2², itd.).
• 3. Pomnóż każdą cyfrę przez jej wagę.
• 4. Zsumuj wszystkie uzyskane wartości.
• 5. Otrzymasz wartość dziesiętną.

Krok po kroku: przeliczanie binarnej liczby 1010 na dziesiętną

Przykład przeliczenia liczby binarnej 1010 na system dziesiętny jest prosty i ilustruje proces w praktyce. Rozpoczynamy od zapisania liczby 1010. Od prawej do lewej mamy: 0 (2⁰), 1 (2¹), 0 (2²), 1 (2³). Teraz wykonujemy mnożenie: 0 * 1 = 0, 1 * 2 = 2, 0 * 4 = 0, 1 * 8 = 8. Następnie sumujemy te wartości: 0 + 2 + 0 + 8 = 10. W ten sposób liczba binarna 1010 odpowiada liczbie dziesiętnej 10.

Jak konwertować liczby dziesiętne na binarne bez trudności

Konwersja liczb dziesiętnych na binarne jest procesem, który można zrealizować w kilku prostych krokach. Podstawową metodą jest dzielenie liczby dziesiętnej przez 2, a następnie zapisywanie reszt z tych dzielenia. Reszty te odczytuje się w odwrotnej kolejności, co pozwala uzyskać wynik w systemie binarnym. Dzięki temu, nawet osoby bez zaawansowanej wiedzy matematycznej mogą łatwo przekształcić liczby dziesiętne na binarne.

Na przykład, aby przekształcić liczbę 13 na system binarny, dzielimy ją przez 2. Pierwsze dzielenie daje 6 z resztą 1, następnie 6 dzielimy przez 2, co daje 3 z resztą 0. Kontynuując, 3 dzielimy przez 2, co daje 1 z resztą 1, a na końcu 1 dzielimy przez 2, co daje 0 z resztą 1. Odczytując reszty w odwrotnej kolejności, otrzymujemy 1101, co oznacza, że liczba dziesiętna 13 w systemie binarnym to 1101.

Aby ułatwić konwersję, można skorzystać z poniższej listy popularnych liczb dziesiętnych i ich odpowiedników w systemie binarnym:

• 0 - 0
• 1 - 1
• 2 - 10
• 3 - 11
• 4 - 100
• 5 - 101
• 6 - 110
• 7 - 111
• 8 - 1000
• 9 - 1001
• 10 - 1010
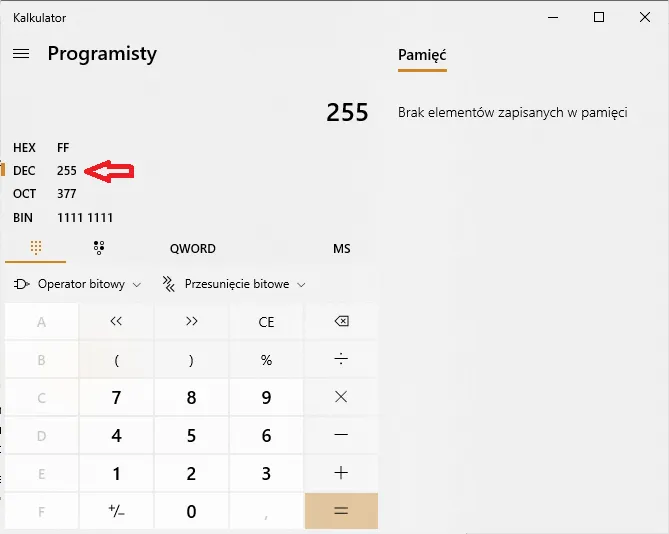
• 255 - 11111111

Przykład: przekształcanie liczby 255 na system binarny

Aby przekształcić liczbę 255 na system binarny, zaczynamy od dzielenia przez 2. Pierwsze dzielenie 255 przez 2 daje 127 z resztą 1. Kolejne dzielenie 127 przez 2 daje 63 z resztą 1. Następnie 63 dzielimy przez 2, co daje 31 z resztą 1. Kontynuując, 31 dzielimy przez 2, co daje 15 z resztą 1, a 15 dzielimy przez 2, co daje 7 z resztą 1. Potem 7 dzielimy przez 2, co daje 3 z resztą 1, a 3 dzielimy przez 2, co daje 1 z resztą 1. Na końcu 1 dzielimy przez 2, co daje 0 z resztą 1. Odczytując reszty w odwrotnej kolejności, otrzymujemy 11111111, co oznacza, że liczba dziesiętna 255 w systemie binarnym to 11111111.

Jak wykonywać operacje arytmetyczne w systemie binarnym

W systemie binarnym można wykonywać podstawowe operacje arytmetyczne, takie jak dodawanie i odejmowanie. Te operacje są nieco inne niż w systemie dziesiętnym, ponieważ opierają się na dwóch cyfrach: 0 i 1. Dodawanie w systemie binarnym polega na sumowaniu cyfr, a wynik może wymagać przeniesienia, gdy suma przekracza 1. Podobnie, odejmowanie w systemie binarnym również wymaga zrozumienia, jak działa przeniesienie, ale w przeciwnym kierunku.

Podczas dodawania, zasady są proste: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, a 1 + 1 = 10 (co oznacza 0 i przeniesienie 1). W przypadku odejmowania, zasady są podobne, ale musimy pamiętać, że 0 - 1 nie jest możliwe, co wymaga pożyczania. Te różnice sprawiają, że operacje w systemie binarnym są fascynujące i wymagają dokładności.

Dodawanie i odejmowanie w systemie binarnym - praktyczne przykłady

Aby lepiej zrozumieć dodawanie w systemie binarnym, weźmy przykład: 1011 (11 w systemie dziesiętnym) + 1101 (13 w systemie dziesiętnym). Zaczynamy od prawej strony: 1 + 1 = 10, zapisujemy 0 i przenosimy 1. Następnie 1 + 0 + 1 (przeniesienie) = 10, zapisujemy 0 i przenosimy 1. Kolejnie 1 + 1 + 1 (przeniesienie) = 11, zapisujemy 1 i przenosimy 1. Na koniec 1 (przeniesienie) + 1 = 10, zapisujemy 0 i przenosimy 1. Ostateczny wynik to 11000, co oznacza 24 w systemie dziesiętnym.

Przykład odejmowania: 1100 (12 w systemie dziesiętnym) - 1010 (10 w systemie dziesiętnym). Zaczynamy od prawej: 0 - 0 = 0. Następnie 0 - 1 nie jest możliwe, więc pożyczamy 1, co zmienia 1 na 0 i daje nam 2. Ostatecznie 2 - 1 = 1. Potem 0 - 0 = 0. Ostateczny wynik to 10, co oznacza 2 w systemie dziesiętnym.

Operacja	Wynik
1011 + 1101	11000
1100 - 1010	10

Jakie są praktyczne zastosowania systemu binarnego w technologii

System binarny ma kluczowe znaczenie w różnych technologiach, zwłaszcza w obszarze informatyki i komunikacji cyfrowej. Jego zastosowanie obejmuje wszystko, od prostych urządzeń, takich jak kalkulatory, po zaawansowane systemy komputerowe. W każdym przypadku, system binarny umożliwia efektywne przechowywanie i przetwarzanie danych, co jest niezbędne w nowoczesnym świecie technologicznym. Przykłady zastosowań obejmują programowanie, kodowanie danych oraz transmisję sygnałów w sieciach komputerowych.

W kontekście komunikacji, system binarny jest wykorzystywany do kodowania informacji w formie bitów. Każda informacja przesyłana przez Internet, w tym teksty, obrazy i filmy, jest konwertowana na wartości binarne, co pozwala na ich efektywne przesyłanie i przechowywanie. Bez systemu binarnego nie byłoby możliwe funkcjonowanie takich technologii jak Wi-Fi, Bluetooth czy sieci komórkowe.

Rola systemu binarnego w komputerach i urządzeniach cyfrowych

System binarny jest podstawą działania komputerów i innych urządzeń cyfrowych. W każdym komputerze, procesor interpretuje dane jako zbiory bitów, co pozwala na wykonywanie obliczeń i operacji logicznych. Na przykład, pamięć RAM przechowuje dane w postaci binarnej, co umożliwia szybki dostęp do informacji. Dzięki temu, komputery mogą wykonywać skomplikowane zadania w krótkim czasie.

Warto również zauważyć, że urządzenia takie jak smartfony, tablety i aparaty cyfrowe również korzystają z systemu binarnego. Każde zdjęcie, które robimy, jest kodowane w postaci binarnej, co pozwala na jego przechowywanie i przesyłanie. Bez systemu binarnego, nowoczesne technologie, które znamy i używamy na co dzień, nie mogłyby istnieć.

• Komputery - przetwarzanie danych i wykonywanie obliczeń.
• Smartfony - przechowywanie i przesyłanie informacji w formie binarnej.
• Aparaty cyfrowe - kodowanie zdjęć jako dane binarne.
• Routery - przesyłanie sygnałów w sieciach komunikacyjnych.
• Urządzenia IoT - komunikacja i wymiana danych w systemach domowych.

Przyszłość systemu binarnego w technologii kwantowej i AI

W miarę jak technologia kwantowa staje się coraz bardziej popularna, system binarny zyskuje nowe zastosowania w kontekście obliczeń kwantowych. W przeciwieństwie do tradycyjnych systemów obliczeniowych, które opierają się na bitach, komputery kwantowe wykorzystują kubity, które mogą reprezentować zarówno 0, jak i 1 jednocześnie dzięki zjawisku znanemu jako superpozycja. To otwiera drzwi do złożonych obliczeń, które są nieosiągalne dla klasycznych komputerów, co może znacząco wpłynąć na rozwój sztucznej inteligencji.

W kontekście AI, połączenie technologii kwantowej z systemem binarnym może przyspieszyć procesy uczenia maszynowego. Algorytmy mogą wykorzystywać moc obliczeniową komputerów kwantowych do szybszego przetwarzania dużych zbiorów danych, co może prowadzić do bardziej zaawansowanych i precyzyjnych modeli predykcyjnych. W przyszłości możemy spodziewać się, że rozwój tych technologii zrewolucjonizuje sposób, w jaki przetwarzamy informacje i podejmujemy decyzje w różnych dziedzinach, od medycyny po finansowe analizy.